[题目]如图.某海防哨所发现在它的北偏西.距离为的处有一艘船.该船向正东方向航行.经过到达哨所东北方向的处.则该船的航速为每小时．(精确到) 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，某海防哨所发现在它的北偏西，距离为的处有一艘船，该船向正东方向航行，经过到达哨所东北方向的处，则该船的航速为每小时___．（精确到）

【答案】

【解析】

设AB与正北方向线交于点C，根据已知及三角函数求得AC、OC的长，再根据等腰直角三角形的性质求得BC的长，利用AB=AC+BC求出AB的长，再除以该船航行的时间即可求解．

设AB与正北方向线交于点C，

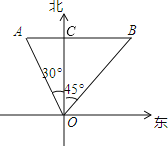
∵在直角△AOC中，∠AOC=30°，OA=500米，

∴AC=OAsin30°=250米，OC=OAcos30°=250米，

∵直角△OBC是等腰直角三角形，

∴BC=OC=250米，

∴AB=AC+BC=250+250（米），

∴该船的航速为=5+5≈13.7（千米/时），

即该船的航速约为每小时13.7千米．

故答案为13.7．

练习册系列答案

A. 4B. 3C. 2D. 1

【题目】（2011山东济南，27，9分）如图，矩形OABC中，点O为原点，点A的坐标为（0，8），点C的坐标为（6，0）．抛物线经过A、C两点，与AB边交于点D．

（1）求抛物线的函数表达式；

（2）点P为线段BC上一个动点（不与点C重合），点Q为线段AC上一个动点，AQ=CP，连接PQ，设CP=m，△CPQ的面积为S．

①求S关于m的函数表达式，并求出m为何值时，S取得最大值；

②当S最大时，在抛物线的对称轴l上若存在点F，使△FDQ为直角三角形，请直接写出所有符合条件的F的坐标；若不存在，请说明理由．

【题目】元旦放假期间，小明和小华准备到西安的大雁塔（记为A）、白鹿原（记为B）、兴庆公园（记为C）、秦岭国家植物园（记为D）中的一个景点去游玩，他们各自在这四个景点中任选一个，每个景点被选中的可能性相同

（1）求小明选择去白鹿原游玩的概率；

（2）用树状图或列表的方法求小明和小华选择去同一个地方游玩的概率．

【题目】如图，已知△ABC，按以下步骤作图：①分别以 B，C 为圆心，以大于BC 的长为半径作弧，两弧相交于两点 M，N；②作直线 MN 交 AB 于点 D，连接 CD．若 CD=AC，∠A=50°，则∠ACB 的度数为

A.90°B.95°C.105°D.110°

【题目】有5张背面看上去无差别的扑克牌，正面分别写着5，6，7，8，9，洗匀后正面向下放在桌子上，从中随机抽取2张，抽出的卡片上的数字恰好是两个连续整数的概率是__．

【题目】某教育局组织了“落实十九大精神，立足岗位见行动”教师演讲比赛，根据各校初赛成绩在小学组、中学组分别选出10名教师参加决赛，这些选手的决赛成绩如图所示：

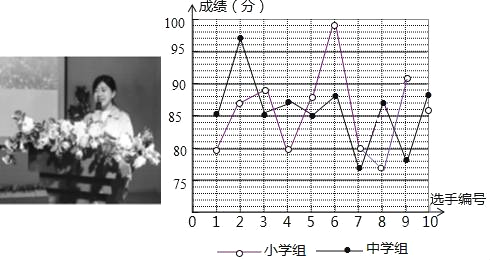
根据上图提供的信息，回答下列问题：

（1）请你把下面表格填写完整：

团体成绩	众数	平均数	方差
小学组		85.7	39.6
中学组	85		27.8

（2）考虑平均数与方差，你认为哪个组的团体成绩更好些，并说明理由；

（3）若在每组的决赛选手中分别选出3人参加总决赛，你认为哪个组获胜的可能性大些？请说明理由．

【题目】如图，△ABC是等边三角形，点D是BC边上一动点，点E，F分别在AB，AC边上，连接AD，DE，DF，且∠ADE=∠ADF=60°．

小明通过观察、实验，提出猜想：在点D运动的过程中，始终有AE=AF，小明把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：

想法1：利用AD是∠EDF的角平分线，构造△ADF的全等三角形，然后通过等腰三角形的相关知识获证．

想法2：利用AD是∠EDF的角平分线，构造角平分线的性质定理的基本图形，然后通过全等三角形的相关知识获证．

想法3：将△ACD绕点A顺时针旋转至△ABG，使得AC和AB重合，然后通过全等三角形的相关知识获证．

请你参考上面的想法，帮助小明证明AE=AF．（一种方法即可）

【题目】如图所示，在平面直角坐标中，四边形OABC是梯形，且AB = OC = 4，CB∥OA，OA = 7，∠COA = 60°，点P为x轴上的—个动点，点P不与点0、点A重合．连结CP，过点P作PD交AB于点D，

（1）求点B的坐标；

（2）当点P运动什么位置时，使得∠CPD =∠OAB，且，求这时点P的坐标；

（3）当点P运动什么位置时，△OCP为等腰三角形，直接写出这时点P的坐标。

试题分类