题目内容
【题目】已知:如图,在平面直角坐标系xOy中,抛物线y=ax2﹣4ax+1与x轴的正半轴交于点A和点B,与y轴交于点C,且OB=3OC,点P是第一象限内的点,连接BC,△PBC是以BC为斜边的等腰直角三角形.
(1)求这个抛物线的表达式;
(2)求点P的坐标;
(3)点Q在x轴上,若以Q、O、P为顶点的三角形与以点C、A、B为顶点的三角形相似,求点Q的坐标.

【答案】(1)![]() ;(2)P(2,2);(3)(﹣4,0)或(﹣2,0).
;(2)P(2,2);(3)(﹣4,0)或(﹣2,0).
【解析】
试题分析:(1)利用待定系数法即可得出结论;
(2)先判断出△PMC≌△PNB,再用PC2=PB2,建立方程求解即可;
(3)先判断出点Q只能在点O左侧,再分两种情况讨论计算即可.
试题解析:(1)∵抛物线y=ax2﹣4ax+1,∴点C的坐标为(0,1).
∵OB=3OC,∴点B的坐标为(3,0),∴9a﹣12a+1=0,∴a=![]() ,∴
,∴![]() .
.
(2)如图,过点P作PM⊥y轴,PN⊥x轴,垂足分别为点M、N.
∵∠MPC=90°﹣∠CPN,∠NPB=90°﹣∠CPN,∴∠MPC=∠NPB.
在△PCM和△PBN中,∵∠PMC=∠PNB,∠MPC=∠NPB,PC=PB,∴△PMC≌△PNB,∴PM=PN.
设点P(a,a).
∵PC2=PB2,∴a2+(a﹣1)2=(a﹣3)2+a2.
解得a=2,∴P(2,2).
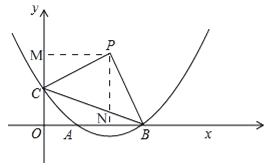
(3)∵该抛物线对称轴为x=2,B(3,0),∴A(1,0).
∵P(2,2),A(1,0),B(3,0),C(0,1),∴PO=![]() ,AC=
,AC=![]() ,AB=2.
,AB=2.
∵∠CAB=135°,∠POB=45°,在Rt△BOC中,tan∠OBC=![]() ,∴∠OBC≠45°,∠OCB<90°,在Rt△OAC中,OC=OA,∴∠OCA=45°,∴∠ACB<45°,∴当△OPQ与△ABC相似时,点Q只有在点O左侧时.
,∴∠OBC≠45°,∠OCB<90°,在Rt△OAC中,OC=OA,∴∠OCA=45°,∴∠ACB<45°,∴当△OPQ与△ABC相似时,点Q只有在点O左侧时.
(i)当![]() 时,∴
时,∴![]() ,∴OQ=4,∴Q(﹣4,0).
,∴OQ=4,∴Q(﹣4,0).
(ii)当![]() 时,∴
时,∴![]() ,∴OQ=2,∴Q(﹣2,0).
,∴OQ=2,∴Q(﹣2,0).
当点Q在点A右侧时,综上所述,点Q的坐标为(﹣4,0)或(﹣2,0).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案