Question

【题目】如图，在△ABC中，∠ABC=60°，∠ACB=45°，AD、CF都是高，相交于点P，角平分线BE分别交AD、CF于Q、S，则图中的等腰三角形个数是（ ）

A.2
B.3
C.4
D.5

Answer 1

【答案】D
【解析】解：∵∠ABC=60°，∠ACB=45°，AD、CF都是高，
∴∠DAC=45°，
∴CD=AD，
∴△ADC为等腰直角三角形，
∴∠BAD=30°，
∴∠APF=60°，
∵∠ABC=60°，且BE是∠ABC的角平分线，
∴∠QBD=30°，
∴∠BQD=60°，
∴SP=SQ，
∴△QSP为等腰三角形，
∵∠BAD=EBA=30°，
∴△QAB是等腰三角形，
∵∠ABE=30°，∠AEB=∠EBC+∠ACD=30°+45°=75°，
∴∠BAC=180°﹣30°﹣75°=75°，
∴∠BAC=∠AEB，
∴△ABE是等腰三角形，
∵∠SBC=∠SCB=30°，
∴△SBC是等腰三角形，
故选D．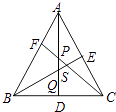

【考点精析】本题主要考查了等腰三角形的判定的相关知识点，需要掌握如果一个三角形有两个角相等，那么这两个角所对的边也相等（简称：等角对等边）．这个判定定理常用于证明同一个三角形中的边相等才能正确解答此题．