Question

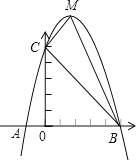
【题目】如图，在平面直角坐标系中，直线y＝x+1与抛物线y＝x2+bx+c交于A，B（4，5）两点，点A在x轴上．

（1）求抛物线的解析式；

（2）点E是线段AB上一动点（点A，B除外），过点E作x轴的垂线交抛物线于点F，当线段EF的长度最大时，求点E的坐标；

（3）在（2）的条件下，抛物线上是否存在一点P，使∠PEF＝90°？若存在，求出点P的坐标；若不存在，说明理由．

Answer 1

【答案】（1）抛物线的解析式为y=x2-2x-3；（2）E（，）；点P的坐标为（1-，）或（1+，）．

【解析】

（1）先求得点A的坐标，然后将点A和点B的坐标代入抛物线的解析式可得到关于b、c的方程组，从而可求得b、c的值；

（2）设点E的坐标为（x，x+1），则点F的坐标为F（x，x2-2x-3），则可得到EF与x的函数关系式，利用配方法可求得EF的最大值以及点E的坐标；

（3）过点E作PE⊥EF，交抛物线与点P或点P′，则yp=，将y=代入抛物线的解析式得：x2-2x-3=，然后可求得点P的横坐标．

（1）把y=0代入y=x+1得：x+1=0，解得：x=-1，

∴点A（-1，0）．

将点A和点B的坐标代入抛物线的解析式得：

，

解得：b=-2，c=-3．

∴抛物线的解析式为y=x2-2x-3．

（2）如图1所示：

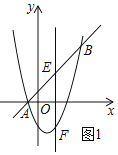
设点E的坐标为（x，x+1），则点F的坐标为F（x，x2-2x-3）．

设EF=（x+1）-（x2-2x-3）=-x2+3x+4=-（x-）2+．

∴当x=时，EF有最大值．

将x=代入y=x+1得：y=．

∴E（，）．

（3）如图2所示：过点E作PE⊥EF，交抛物线与点P或点P′，则yp=．

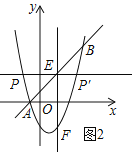
将y=代入抛物线的解析式得：x2-2x-3=，解得：x=1+，x=1-．

∴点P的坐标为（1-，）或（1+，）．