题目内容
【题目】右图中曲线是反比例函数 
的图象的一支．
（1）这个反比例函数图象的另一支位于哪个象限？常数n的取值范围是什么？
（2）若一次函数 
的图象与反比例函数的图象交于点A，与x轴交于点B，△AOB的面积为2，求n的值．
【答案】
（1）
解：这个反比例函数图象的另一支位于第四象限．
由n+7＜0，
解得n＜﹣7，
即常数n的取值范围是n＜﹣7
（2）
解：在 
中令y=0，得x=2，
即OB=2．
过A作x轴的垂线，垂足为C，如图．
∵S△AOB=2，即 
OBAC=2，
∴ ×2×AC=2，解得AC=2，即A点的纵坐标为2．
把y=2代入 中，得x=﹣1，即A（﹣1，2）．
所以 
，
解得n=﹣9
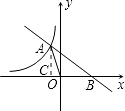
【解析】（1）根据反比例函数的性质可求得反比例函数的图象分布在第二、第四象限，所以n+7＜0即可求解；（2）图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S= |k|，可利用△AOB的面积求出n值．
【考点精析】关于本题考查的反比例函数的图象和反比例函数的性质，需要了解反比例函数的图像属于双曲线．反比例函数的图象既是轴对称图形又是中心对称图形．有两条对称轴：直线y=x和 y=-x．对称中心是：原点；性质:当k＞0时双曲线的两支分别位于第一、第三象限，在每个象限内y值随x值的增大而减小； 当k＜0时双曲线的两支分别位于第二、第四象限，在每个象限内y值随x值的增大而增大才能得出正确答案．
【题目】鲁班家装公司为芙蓉小区做家装设计，调查员设计了如下问卷，对家装风格进行专项调查． 
通过随机抽样调查50家客户，得到如下数据：
A B B A B B A C A C A B A D A A B
B A A D B A B A C A C B A A D A A
A B B D A A A B A C A B D A B A
（1）请你补全下面的数据统计表： 家装风格统计表
装修风格 | 划记 | 户数 | 百分比 |
A中式 | 正正正正正 | 25 | 50% |
B欧式 | |||
C韩式 | 5 | 10% | |
D其他 | 正 | 10% | |
合计 | 50 | 100% |
（2）请用扇形统计图描述（1）表中的统计数据；（注：请标明各部分的圆心角度数）
（3）如果公司准备招聘10名装修设计师，你认为各种装修风格的设计师应分别招多少人？
