题目内容
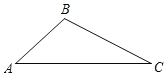
【题目】问题情景：数学课上，老师布置了这样一道题目，如图1，△ABC是等边三角形，点D是BC的中点，且满足∠ADE＝60°，DE交等边三角形外角平分线于点E．试探究AD与DE的数量关系．
操作发现：（1）小明同学过点D作DF∥AC交AB于F，通过构造全等三角形经过推理论证就可以解决问题，请您按照小明同学的方法确定AD与DE的数量关系，并进行证明．
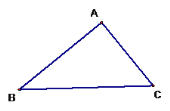
类比探究：（2）如图2，当点D是线段BC上任意一点(除B、C外)，其他条件不变，试猜想AD与DE之间的数量关系，并证明你的结论．
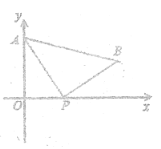
拓展应用：（3）当点D在线段BC的延长线上，且满足CD＝BC，在图3中补全图形，直接判断△ADE的形状(不要求证明)．
【答案】（1）AD＝DE，见解析；（2）AD＝DE，见解析；（3）见解析，△ADE是等边三角形，
【解析】
（1）根据题意，通过平行线的性质及等边三角形的性质证明
即可得解；
（2）根据题意，通过平行线的性质及等边三角形的性质证明
即可得解；
（3）根据垂直平分线的性质及等边三角形的判定定理进行证明即可.
（1）如下图，数量关系：AD＝DE.
证明：∵
是等边三角形
∴AB＝BC，
∵DF∥AC
∴
，∠BDF＝∠BCA
∴
∴
是等边三角形，
∴DF＝BD
∵点D是BC的中点
∴BD＝CD
∴DF＝CD
∵CE是等边的外角平分线
∴
∵是等边三角形，点D是BC的中点
∴AD⊥BC
∴
∵
∴
在
与
中
∴
∴AD＝DE；
（2）结论：AD＝DE.
证明：如下图，过点D作DF∥AC，交AB于F
∵是等边三角形
∴AB＝BC，
∵DF∥AC
∴
∴
∴是等边三角形，
∴BF＝BD
∴AF＝DC
∵CE是等边的外角平分线
∴
∵∠ADC是
的外角
∴
∵
∴∠FAD＝∠CDE
在
与
中
∴
∴AD＝DE；
（3）如下图，
是等边三角形.
证明：∵
∴
∵CE平分
∴CE垂直平分AD
∴AE=DE
∵
∴是等边三角形.
