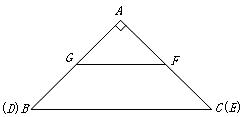
题目内容
如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,另有一等腰梯形
,另有一等腰梯形![]() (
(![]() )的底边
)的底边![]() 与
与![]() 重合,两腰分别落在
重合,两腰分别落在![]() 上,且
上,且![]() 分别是
分别是![]() 的中点.
的中点.
(1)求等腰梯形![]() 的面积;
的面积;
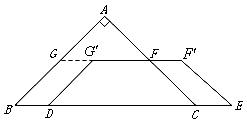
(2)操作:固定![]() ,将等腰梯形
,将等腰梯形![]() 以每秒1个单位的速度沿
以每秒1个单位的速度沿![]() 方向向右运动,直到点
方向向右运动,直到点![]() 与点
与点![]() 重合时停止.设运动时间为
重合时停止.设运动时间为![]() 秒,运动后的等腰梯形为
秒,运动后的等腰梯形为![]() (如图).
(如图).
探究1:在运动过程中,四边形![]() 能否是菱形?若能,请求出此时
能否是菱形?若能,请求出此时![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
探究2:设在运动过程中![]() 与等腰梯形
与等腰梯形![]() 重叠部分的面积为
重叠部分的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式.
的函数关系式.
解:如图,(1)过点![]() 作
作![]() 于
于![]() .
.
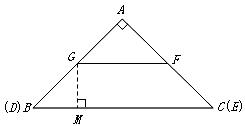
![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 中点
中点
![]() .
.
又![]() 分别为
分别为![]() 的中点
的中点
![]()
![]()
![]() 等腰梯形
等腰梯形![]() 的面积为6.
的面积为6.
(2)能为菱形
如图,由![]() ,
,![]()
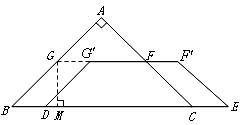
![]() 四边形
四边形![]() 是平行四边形
是平行四边形
当![]() 时,四边形
时,四边形![]() 为菱形,
为菱形,
此时可求得![]()
![]() 当
当![]() 秒时,四边形
秒时,四边形![]() 为菱形.
为菱形.
(3)分两种情况:
①当![]() 时,
时,
方法一:![]() ,
,![]()
![]() 重叠部分的面积为:
重叠部分的面积为:![]()
![]() 当
当![]() 时,
时,![]() 与
与![]() 的函数关系式为
的函数关系式为![]()
方法二:当![]() 时,
时,
![]() ,
,![]() ,
,![]()
![]() 重叠部分的面积为:
重叠部分的面积为:
![]()
![]() 当
当![]() 时,
时,![]() 与
与![]() 的函数关系式为
的函数关系式为![]()
②当![]() 时,
时,
设![]() 与
与![]() 交于点
交于点![]() ,则
,则![]()
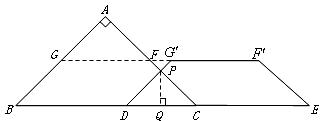
![]() ,
,![]()
作![]() 于
于![]() ,则
,则![]()
![]() 重叠部分的面积为:
重叠部分的面积为:
![]()

练习册系列答案
相关题目
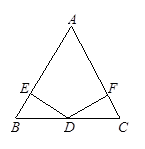
 ≌
≌ (③ )
(③ ) 中,AB= AC,D是底边BC的中点,作DE⊥AB于E,DF⊥AC于F
中,AB= AC,D是底边BC的中点,作DE⊥AB于E,DF⊥AC于F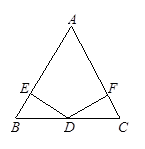
 (① )
(① ) BDE和
BDE和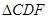 中,
中,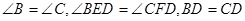 ,
,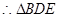 ≌
≌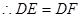 (③ )
(③ )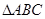 中,AB= AC,D是底边BC的中点,作DE⊥AB于E,DF⊥AC于F
中,AB= AC,D是底边BC的中点,作DE⊥AB于E,DF⊥AC于F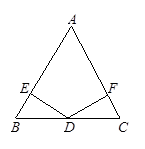
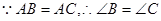 (① )
(① )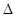 BDE和
BDE和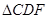 中,
中,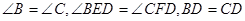 ,
,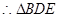 ≌
≌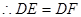 (③ )
(③ ) 中,
中, ,
, ,
, ,AF=10cm, AC=14cm,动点E以2cm/s的速度从
,AF=10cm, AC=14cm,动点E以2cm/s的速度从 点向
点向 点运动,动点
点运动,动点 以1cm/s的速度从
以1cm/s的速度从 点向
点向
 ;
; 与
与 全等;
全等; ,
,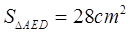 ,求
,求 。
。