题目内容
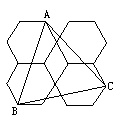
如图，在矩形ABCD中，AB的长度为a，BC的长度为b，其中
b＜a＜b．将此矩形纸片按下列顺序折叠，则C′D′的长度为 （用含a、b的代数式表示）．
b＜a＜b．将此矩形纸片按下列顺序折叠，则C′D′的长度为 （用含a、b的代数式表示）．3a﹣2b
由轴对称可以得出A′B=AB=a，就有A′C=b﹣a，从而就有A′C′=b﹣a，就可以得出C′D′=a﹣2（b﹣a），化简就可以得出结论．
解：由轴对称可以得出A′B=AB=a，
∵BC=b，
∴A′C=b﹣a．
由轴对称可以得出A′C′=b﹣a，
∴C′D′=a﹣2（b﹣a），
∴C′D′=3a﹣2b．
故答案为：3a﹣2b．
解：由轴对称可以得出A′B=AB=a，
∵BC=b，
∴A′C=b﹣a．
由轴对称可以得出A′C′=b﹣a，
∴C′D′=a﹣2（b﹣a），
∴C′D′=3a﹣2b．
故答案为：3a﹣2b．
练习册系列答案
阅读快车系列答案
相关题目
