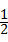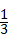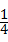题目内容
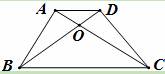
如图,梯子共有7级互相平行的踏板,每相邻两级踏板之间的距离都相等.已知梯子最上面一级踏板的长度A1B1 = 0.5m,最下面一级踏板的长度A7B7 = 0.8m.则第五级踏板A5B5的长度为 ( )


| A.0.6m | B.0.65m | C.0.7m | D.0.75m |
C
根据梯形中位线定理和相似三角形的性质解答.
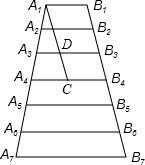
解:因为每相邻两级踏板之间的距离都相等,
所以A4B4为梯形A1A7B7B1的中位线,
根据梯形中位线定理,
A4B4=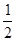 (A1B1+A7B7)=
(A1B1+A7B7)=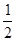 (0.5+0.8)=0.65m.
(0.5+0.8)=0.65m.
作A1C∥B1B4,
则DB3=CB4=A1B1=0.5m,
A4C=0.65cm-0.50cm=0.15cm,
于是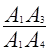 =
= ,
,
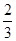 =
=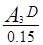 ,
,
解得A3D=0.10m.
A3B3=0.10cm+0.50cm=0.60m.
故选:C.
本题考查了梯形中位线定理和相似三角形性质的应用.解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决

解:因为每相邻两级踏板之间的距离都相等,
所以A4B4为梯形A1A7B7B1的中位线,
根据梯形中位线定理,
A4B4=
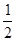 (A1B1+A7B7)=
(A1B1+A7B7)=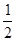 (0.5+0.8)=0.65m.
(0.5+0.8)=0.65m.作A1C∥B1B4,
则DB3=CB4=A1B1=0.5m,
A4C=0.65cm-0.50cm=0.15cm,
于是
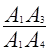 =
= ,
,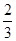 =
=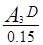 ,
,解得A3D=0.10m.
A3B3=0.10cm+0.50cm=0.60m.
故选:C.
本题考查了梯形中位线定理和相似三角形性质的应用.解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
 的图象与反比例函数
的图象与反比例函数 的图象交于
的图象交于 两点,与
两点,与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,已知
,已知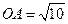 ,
, ,点
,点 的坐标为
的坐标为 .
. ,使得
,使得 与
与 相似,请你求出
相似,请你求出

 灯罩底
灯罩底 面半径MK的长;
面半径MK的长;

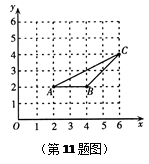
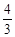 )
)
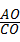 值为( )
值为( )