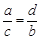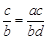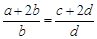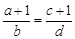题目内容
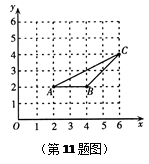
如图,△ABC三个顶点的坐标分别为A(2,2),B(4,2),C(6,4),以原
点O为位似中心,将△ABC缩小,使变换后得到的△DEF与△ABC对应边的比为1∶3,
则点C变换后对应的点的坐标为
点O为位似中心,将△ABC缩小,使变换后得到的△DEF与△ABC对应边的比为1∶3,
则点C变换后对应的点的坐标为

| A.(3,2) | B.(-3,-2)或(3,2) |
C.(2,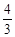 ) ) | D.(2,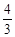 )或(-2,- )或(-2,-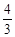 ) ) |
D
位似变换中对应点的坐标的变化规律:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.本题中k=2或-2.
解:∵两个图形的位似比是1:(-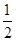 )或1:
)或1: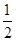 ,AC的中点是(4,3),
,AC的中点是(4,3),
∴对应点是(2,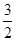 )或(-2,-
)或(-2,-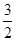 ).
).
解:∵两个图形的位似比是1:(-
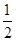 )或1:
)或1: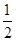 ,AC的中点是(4,3),
,AC的中点是(4,3),∴对应点是(2,
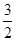 )或(-2,-
)或(-2,-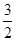 ).
).
练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
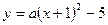 , C2:
, C2: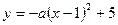 ,C1与C2的交点为A,
,C1与C2的交点为A,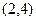 ,点B的横坐标是-2.
,点B的横坐标是-2.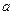 的值及点B的坐标;
的值及点B的坐标; 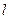 ,且
,且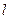 过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;
过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;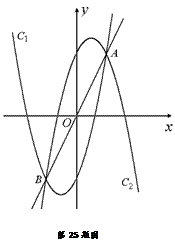
 ,把△BCE沿折痕EC向上翻折,若点B恰好落在AD边上,设这个点为F,则(1)AB= ▲ ,BC= ▲ ;(2)若⊙O内切于以F、E、B、C为顶点的四边形,则⊙O的面积= ▲ .
,把△BCE沿折痕EC向上翻折,若点B恰好落在AD边上,设这个点为F,则(1)AB= ▲ ,BC= ▲ ;(2)若⊙O内切于以F、E、B、C为顶点的四边形,则⊙O的面积= ▲ .


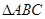 中,
中, 、
、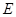 是
是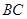 边上的点,
边上的点,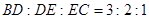 ,
,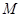 在
在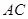
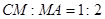 ,
,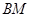 交
交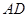 、
、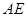 于
于 、
、 ,则
,则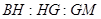 等于 ( )
等于 ( )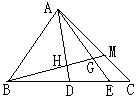
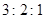
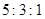
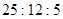
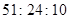
 ,则OD∶
,则OD∶ =
= 
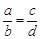 ,那么下列各式中一定成立的是( )
,那么下列各式中一定成立的是( )