题目内容
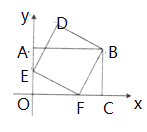
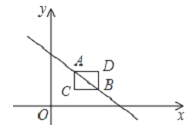
【题目】如图,过点C(2,1)分别作x轴、y轴的平行线,交直线y=﹣x+4于B、A两点,若二次函数y=ax2+bx+c的图象经过坐标原点O,且顶点在矩形ADBC内(包括边上),则a的取值范围是____.
【答案】![]()
【解析】
由过点C(2,1)分别作x轴、y轴的平行线,交直线y=-x+4于B、A两点,即可求得点A与B的坐标,继而求得点D的坐标,又由二次函数y=ax2+bx+c(a≠0)的图象经过坐标原点O,且顶点在矩形ADBC内(包括三边上),可得a<0,然后由|a|越大,开口越小,可得当顶点在顶点在AC上时,a最小,当顶点在顶点在BD上时,a最大,继而求得答案.
∵过点C(2,1)分别作x轴、y轴的平行线,交直线y=-x+4于B、A两点,
∴点A(2,2),点B(3,1),
∵四边形ABCD是矩形,
∴D(3,2),
∵二次函数顶点y=ax2+bx+c(a≠0)的图象经过坐标原点O,且在矩形ADBC内(包括三边上),
∴a<0,
∵|a|越大,开口越小,
即a越小,开口越小,
∴当顶点在AC上时,a最小,
设此时顶点坐标为(2,m),且1≤m≤2,
则二次函数的解析式为:y=a(x-2)2+m,
∵二次函数y=ax2+bx+c(a≠0)的图象经过坐标原点O,
∴a(0-2)2+m=0,
解得:a=-![]() ,
,
∴当m=2时,a最小,a=-![]() ,
,
∴当顶点在顶点在BD上时,a最大,
设此时顶点坐标为(3,n),且1≤n≤2,
则二次函数的解析式为:y=a(x-3)2+n,
∵二次函数y=ax2+bx+c(a≠0)的图象经过坐标原点O,
∴a(0-3)2+n=0,
解得:a=-![]() ,
,
∴当n=1时,a最大,a=-![]() ,
,
∴a的取值范围是:-![]() ≤a≤-
≤a≤-![]() .
.
故答案为:-![]() ≤a≤-
≤a≤-![]() .
.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目