题目内容
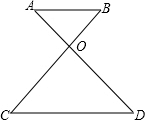（1997•浙江）如图，AB∥CD，AD和BC交于点O，若∠A=42°，∠C=51°，则∠AOB=（ ）分析：先根据平行线的性质求出∠B的度数，再由三角形内角和定理即可得出∠AOB的度数．
解答：解：∵AB∥CD，∠C=51°，
∴∠B=∠C=51°，
在△AOB中，
∵∠A=42°，∠B=51°，
∴∠AOB=180°-∠A-∠B=180°-42°-51°=87°．
故选C．
∴∠B=∠C=51°，
在△AOB中，
∵∠A=42°，∠B=51°，
∴∠AOB=180°-∠A-∠B=180°-42°-51°=87°．
故选C．
点评：本题考查的是平行线的性质，解答此类题目时往往用到三角形的内角和是180°这一隐含条件．
练习册系列答案
相关题目
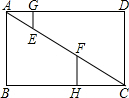（1997•浙江）如图，矩形ABCD中，AB=3，BC=4，线段EF在对角线AC上，EG⊥AD，FH⊥BC，垂足分别是G，H，且EG+FH=EF．
（1997•浙江）如图，?ABCD中，对角线AC和BD交于点O，过O作OE∥BC交DC于点E，若OE=5cm，则AD的长为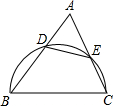
（1997•浙江）如图，锐角△ABC中，以BC为直径的半圆分别交AB，AC于点D，E，记△ADE的面积为S1，△ABC的面积为S2，则
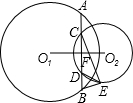（1997•浙江）如图，⊙O1与⊙O2相交，大圆⊙O1的弦AB⊥O1O2，垂足是F，且交⊙O2于点C，D，过B作⊙O2的切线，E为切点，已知BE=DE，BD=m，BE=n，AC，CE的长是关于x的方程x2+px+q=0的两个根．