题目内容
（1997•浙江）如图，?ABCD中，对角线AC和BD交于点O，过O作OE∥BC交DC于点E，若OE=5cm，则AD的长为10
10
cm．分析：由?ABCD中，对角线AC和BD交于点O，OE∥BC，可得OE是△ACD的中位线，根据三角形中位线的性质，即可求得AD的长．
解答：解：∵四边形ABCD是平行四边形，
∴OA=OC，AD∥BC，
∵OE∥BC，
∴OE∥AD，
∴OE是△ACD的中位线，
∴AD=2OE=2×5=10（cm）．
故答案为：10．
∴OA=OC，AD∥BC，
∵OE∥BC，
∴OE∥AD，
∴OE是△ACD的中位线，
∴AD=2OE=2×5=10（cm）．
故答案为：10．
点评：此题考查了平行四边形的性质以及三角形中位线的性质．此题比较简单，注意掌握数形结合思想的应用．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
（1997•浙江）如图，矩形ABCD中，AB=3，BC=4，线段EF在对角线AC上，EG⊥AD，FH⊥BC，垂足分别是G，H，且EG+FH=EF．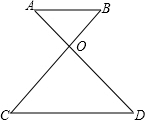
（1997•浙江）如图，AB∥CD，AD和BC交于点O，若∠A=42°，∠C=51°，则∠AOB=（ ）
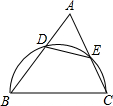（1997•浙江）如图，锐角△ABC中，以BC为直径的半圆分别交AB，AC于点D，E，记△ADE的面积为S1，△ABC的面积为S2，则
（1997•浙江）如图，⊙O1与⊙O2相交，大圆⊙O1的弦AB⊥O1O2，垂足是F，且交⊙O2于点C，D，过B作⊙O2的切线，E为切点，已知BE=DE，BD=m，BE=n，AC，CE的长是关于x的方程x2+px+q=0的两个根．