题目内容
【题目】在平面直角坐标系中，点A(a ,2
)是直线y=
x上一点，以A为圆心，2为半径作⊙A，若P(x,y)是第一象限内⊙A上任意一点，则
的最小值为（ ）
A. 1 B. 
C. 
—1 D. 
【答案】D
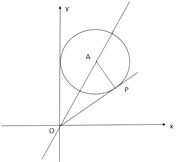
【解析】分析: 如图所示，当直线OP与圆A相切时，连接AP，过P作PH⊥x轴，此时
取得最小值，利用切线的性质得到AP垂直于OP，在直角三角形AOP中，根据到角两边距离相等的点在角的平分线上确定出∠AOP＝30°，
为tan∠30°的值，求出即可．
详解: 如图所示，当直线OP与圆A相切时，连接AP，过P作PH⊥x轴，此时
取得最大值，
∵点A(a ,2
)是直线y=
x上一点，
∴a=2,
∴A(2 ,2
).
∵以A为圆心，2为半径作⊙A，
∴⊙A与y轴相切.
则当直线OP与圆A相切时， 
取得最小值，
∵∠AOy=∠AOP＝30°，
∴∠AOx＝30°，
∴此时
＝tan30°＝
，
则
的最小值为
．
故选：D．
点睛:
此题考查了切线的性质，坐标与图形性质，以及锐角三角函数定义，熟练掌握切线的性质是解本题的关键．
练习册系列答案
相关题目
