题目内容
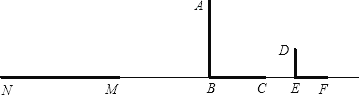
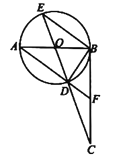
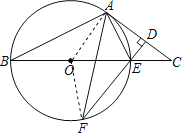
【题目】如图,在△ABC中,点O为BC边上一点,⊙O经过A、B两点,与BC边交于点E,点F为BE下方半圆弧上一点,FE⊥AC,垂足为D,∠BEF=2∠F.
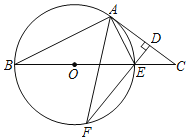
(1)求证:AC为⊙O切线.
(2)若AB=5,DF=4,求⊙O半径长.
【答案】(1)见解析;(2)![]()
【解析】
(1)连结OA,根据已知条件得到∠AOE=∠BEF,根据平行线的性质得到OA⊥AC,于是得到结论;
(2)连接OF,设∠AFE=α,则∠BEF=2α,得到∠BAF=∠BEF=2α,得到∠OAF=∠BAO=α,求得∠AFO=∠OAF=α,根据全等三角形的性质得到AB=AF=5,由勾股定理得到AD=![]() =3,根据圆周角定理得到∠BAE=90°,根据相似三角形的性质即可得到结论.
=3,根据圆周角定理得到∠BAE=90°,根据相似三角形的性质即可得到结论.
解(1)证明:连结OA,
∴∠AOE=2∠F,
∵∠BEF=2∠F,
∴∠AOE=∠BEF,
∴AO∥DF,
∵DF⊥AC,
∴OA⊥AC,
∴AC为⊙O切线;
(2)解:连接OF,
∵∠BEF=2∠F,
∴设∠AFE=α,则∠BEF=2α,
∴∠BAF=∠BEF=2α,
∵∠B=∠AFE=α,
∴∠BAO=∠B=α,
∴∠OAF=∠BAO=α,
∵OA=OF,
∴∠AFO=∠OAF=α,
∴△ABO≌△AFO(AAS),
∴AB=AF=5,
∵DF=4,
∴AD=![]() =3,
=3,
∵BE是⊙O的直径,
∴∠BAE=90°,
∴∠BAE=∠FDA,
∵∠B=∠AFD,
∴△ABE∽△DFA,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴BE=![]() ,
,
∴⊙O半径=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
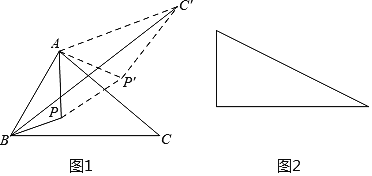
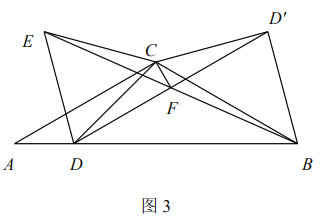
【题目】如图,在![]() 和
和![]() 中,
中,![]() ,点
,点![]() 为射线
为射线![]() ,
,![]() 的交点.
的交点.
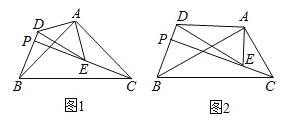
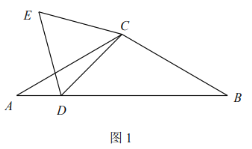
(1)问题提出:如图1,若![]() ,
,![]() .
.
①![]() 与
与![]() 的数量关系为________;
的数量关系为________;
②![]() 的度数为________.
的度数为________.
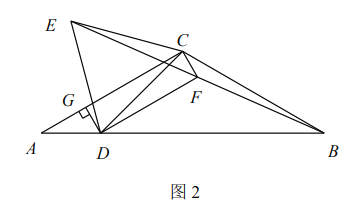
(2)猜想论证:如图2,若![]() ,则(1)中的结论是否成立?请说明理由.
,则(1)中的结论是否成立?请说明理由.