题目内容
【题目】设直线l1和直线l2平行,且l1和l2间的距离为a.如果线段AB在l1的右侧,并设AB关于l1的对称图形是A′B′,而A′B′关于l2的对称图形是A″B″(如图),那么,线段AB和A″B″有什么关系?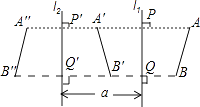
【答案】解:因为l1平行于l2 , 并且AA′A″垂直于l1 , 当然也垂直于l2 , 同理BB′B″也垂直于l1和l2。又在平面内垂直于同一条直线的两条直线互相平行,
所以AA′A″∥BB′B″①
另一方面,因为AP=PA′,A′P′=P′A″,
所以AA′A″=2PP′=2a,
同理BB′B″=2a,
所以AA′A″=BB′B″②
由①②可知,ABB″A'″为平行四边形,所以A'B'平行且等于AB
【解析】轴对称的定义;把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线成轴对称.性质:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线;根据定义和性质可得:AA′=B′B″,A′A″=BB′,所以AA′+A′A″=BB′+B′B″,即
AA″=BB″,而根据l1和l2间的距离为a可得1和l2平行,则根据平行四边形的判断可知AA″B″B为平行四边形,于是可得AA″∥BB″。

练习册系列答案
相关题目