题目内容
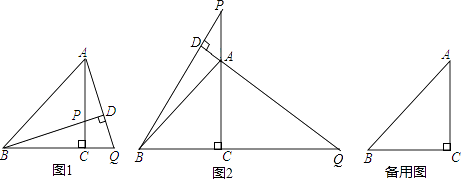
【题目】如图,在△ABC中,∠ABC=36°,∠C=64°,AD平分∠BAC,交BC于D,BE⊥AC,交AD、AC于H、E,且DF∥BE.
求∠FDC和∠AHB的度数.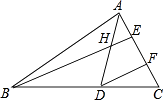
【答案】解:∵BE⊥AC,
∴∠BEC=90°,
∵DF∥BE,
∴∠BEC=∠DFC=90°,
∵∠C=64°,
∴∠FDC=180°﹣(∠DFC+∠C)
=180°﹣(90°+64°)
=26°,
∵∠ABC=36°,∠C=64°,
∴∠BAC=180°﹣∠ABC﹣∠C=180°﹣36°﹣64°=80°,
∵AD平分∠BAC,
∴∠DAC= ![]() ∠BAC=
∠BAC= ![]() ×80°=40°,
×80°=40°,
∴∠AHB=∠DAC+∠BEA
=40°+90°
=130°.
【解析】先根据平行线的性质求出∠C=64°,再根据三角形的内角和定理即可求出结论.
【考点精析】根据题目的已知条件,利用平行线的性质和三角形的内角和外角的相关知识可以得到问题的答案,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某市甲、乙两个汽车销售公司,去年一至十月份每月销售同种品牌汽车的情况如图所示: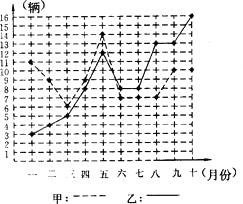
(1)请你根据上图填写下表.
销售公司 | 平均数 | 方差 | 中位数 | 众数 |
甲 | 9 | |||
乙 | 9 | 17.0 | 8 |
(2)请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析:①从平均数和方差结合看;②从折线图上甲、乙两个汽车销售公司销售数量的趋势看(分析哪个汽车销售公司较有潜力).