题目内容
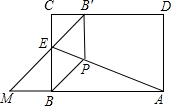 矩形纸片ABCD中,AB=5,AD=4,将纸片折叠,使点B落在边CD上的B′处,折痕为AE.延长B′E交AB的延长线于M,折痕AE上有点P,下列五个结论中正确的有个
矩形纸片ABCD中,AB=5,AD=4,将纸片折叠,使点B落在边CD上的B′处,折痕为AE.延长B′E交AB的延长线于M,折痕AE上有点P,下列五个结论中正确的有个
①∠M=∠DAB′;②PB=PB′;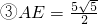 ;④MB′=CD;⑤若B′P⊥CD,则EB′=B′P.
;④MB′=CD;⑤若B′P⊥CD,则EB′=B′P.
- A.2
- B.3
- C.4
- D.5
C
分析:根据∠M=∠CB'E,而∠CB'E+∠DB'A=∠DAB'+∠DB'A=90°可判断①;利用折叠的性质可判断出△B'AP≌△BAP,继而可判断出②;设AE=x,表示出EB'=EB=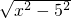 ,在RT△CEB'中利用勾股定理可求出AE的长度,继而可判断出③;利用反证法判断④,最后看得出的结果能证明出来;根据B′P⊥CD,判断出B'P∥BC,从而有∠B'PE=∠BEP=∠B'EP,从而可判断出⑤.综合起来即可得出最终的答案.
,在RT△CEB'中利用勾股定理可求出AE的长度,继而可判断出③;利用反证法判断④,最后看得出的结果能证明出来;根据B′P⊥CD,判断出B'P∥BC,从而有∠B'PE=∠BEP=∠B'EP,从而可判断出⑤.综合起来即可得出最终的答案.
解答:①由题意得∠M=∠CB'E,而∠CB'E+∠DB'A=∠DAB'+∠DB'A=90°,
∴∠M=∠CB'E=∠DAB',故可得①正确;
②根据折叠的性质可得AB'=AB,AP=AP,∠B'AP=∠BAP,从而利用SAS可判定△B'AP≌△BAP,
∴PB=PB',故可得②正确;
③在RT△ADB'可得,B'D= =3,从而可得CB'=5-3=2,
=3,从而可得CB'=5-3=2,
设AE=x,则EB'=EB=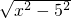 ,
,
在RT△CEB'中,CE2+CB'2=EB'2,即(4-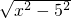 )2+4=x2-25,
)2+4=x2-25,
解得:x= ,即AE=
,即AE= .
.
故可得③正确;
④假如MB′=CD,则可得MB'=AB=AB',
∴∠M=∠BAB',由①得∠M=∠DAB′,
故有∠BAB'=∠DAB',
而本题不能判定∠BAB'=∠DAB',即假设不成立.
故可得④错误.
⑤若B′P⊥CD,则B'P∥BC,
∴∠B'PE=∠BEP=∠B'EP,
∴EB'=B'P,
故可得⑤正确.
综上可得①②③⑤正确,共四个.
故选C.
点评:本题考查了翻折变换,解答过程中涉及了平行四边形的性质、勾股定理,属于综合性题目,解答本题的关键是根据翻折变换的性质得出对应角、对应边分别相等,然后分别判断每个结论,难度较大,注意细心判断.
分析:根据∠M=∠CB'E,而∠CB'E+∠DB'A=∠DAB'+∠DB'A=90°可判断①;利用折叠的性质可判断出△B'AP≌△BAP,继而可判断出②;设AE=x,表示出EB'=EB=
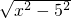 ,在RT△CEB'中利用勾股定理可求出AE的长度,继而可判断出③;利用反证法判断④,最后看得出的结果能证明出来;根据B′P⊥CD,判断出B'P∥BC,从而有∠B'PE=∠BEP=∠B'EP,从而可判断出⑤.综合起来即可得出最终的答案.
,在RT△CEB'中利用勾股定理可求出AE的长度,继而可判断出③;利用反证法判断④,最后看得出的结果能证明出来;根据B′P⊥CD,判断出B'P∥BC,从而有∠B'PE=∠BEP=∠B'EP,从而可判断出⑤.综合起来即可得出最终的答案.解答:①由题意得∠M=∠CB'E,而∠CB'E+∠DB'A=∠DAB'+∠DB'A=90°,
∴∠M=∠CB'E=∠DAB',故可得①正确;
②根据折叠的性质可得AB'=AB,AP=AP,∠B'AP=∠BAP,从而利用SAS可判定△B'AP≌△BAP,
∴PB=PB',故可得②正确;
③在RT△ADB'可得,B'D=
 =3,从而可得CB'=5-3=2,
=3,从而可得CB'=5-3=2,设AE=x,则EB'=EB=
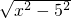 ,
,在RT△CEB'中,CE2+CB'2=EB'2,即(4-
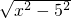 )2+4=x2-25,
)2+4=x2-25,解得:x=
 ,即AE=
,即AE= .
.故可得③正确;
④假如MB′=CD,则可得MB'=AB=AB',
∴∠M=∠BAB',由①得∠M=∠DAB′,
故有∠BAB'=∠DAB',
而本题不能判定∠BAB'=∠DAB',即假设不成立.
故可得④错误.
⑤若B′P⊥CD,则B'P∥BC,
∴∠B'PE=∠BEP=∠B'EP,
∴EB'=B'P,
故可得⑤正确.
综上可得①②③⑤正确,共四个.
故选C.
点评:本题考查了翻折变换,解答过程中涉及了平行四边形的性质、勾股定理,属于综合性题目,解答本题的关键是根据翻折变换的性质得出对应角、对应边分别相等,然后分别判断每个结论,难度较大,注意细心判断.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
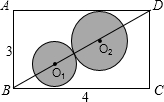 如图,矩形纸片ABCD中,AB=3cm,BC=4cm,若要在该纸片中剪下两个外切的圆⊙O1和⊙O2,要求⊙O1和⊙O2的圆心均在对角线BD上,且⊙O1和⊙O2分别与BC、AD相切,则O1O2的长为( )
如图,矩形纸片ABCD中,AB=3cm,BC=4cm,若要在该纸片中剪下两个外切的圆⊙O1和⊙O2,要求⊙O1和⊙O2的圆心均在对角线BD上,且⊙O1和⊙O2分别与BC、AD相切,则O1O2的长为( )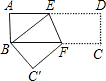 如图,矩形纸片ABCD中,AD=9,AB=3,将其折叠,使点D与点B重合,折痕为EF,那么折痕EF的长为
如图,矩形纸片ABCD中,AD=9,AB=3,将其折叠,使点D与点B重合,折痕为EF,那么折痕EF的长为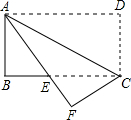 如图,在矩形纸片ABCD中,将矩形纸片沿着对角线AC折叠,使点D落在点F处,设AF与BC相交于点E.
如图,在矩形纸片ABCD中,将矩形纸片沿着对角线AC折叠,使点D落在点F处,设AF与BC相交于点E.