题目内容
【题目】如图，在平行四边形ABCD中，AB＝6cm，BC＝12cm．∠B＝30°．点P在BC上由点B向点C出发，速度为每秒2cm；点Q在边AD上，同时由点D向点A运动，速度为每秒1cm，当点P运动到点C时，P、Q同时停止运动．连接PQ，设运动时间为t秒．
（1）当t为何值时四边形ABPQ为平行四边形？
（2）设四边形ABPQ的面积为y，求y与t之间的函数关系式．
（3）当t为何值时，四边形ABPQ的面积是四边形ABCD的面积的四分之三，并求出此时∠PQD的度数．
（4）连结AP，是否存在某一时刻t，使△ABP为等腰三角形？并求出此刻t的值．
【答案】（1）t＝4s时，四边形ABPQ是平行四边形；（2）y＝
t+18（0＜t≤6）；（3）∠DQP＝75°；（4）当t＝3或
或3时，△ABP为等腰三角形．
【解析】
(1)利用平行四边形的对边相等AQ=BP建立方程求解即可；
(2)先构造直角三角形，求出AE，再用梯形的面积公式即可得出结论；
(3)利用面积关系求出t，即可求出DQ，进而判断出DQ=PQ，即可得出结论；
(4)分三种情况，利用等腰三角形的性质，两腰相等建立方程求解即可得出结论．
解：（1）由运动知，AQ＝12﹣t，BP＝2t，
∵四边形ABPQ为平行四边形，
∴AQ＝BP，
∴12﹣t＝2t
∴t＝4，
即：t＝4s时，四边形ABPQ是平行四边形；
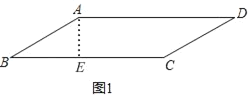
（2）如图1，
过点A作AE⊥BC于E，
在Rt△ABE中，∠B＝30°，AB＝6，
∴AE＝3，
由运动知，BP＝2t，DQ＝t，
∵四边形ABCD是平行四边形，
∴AD＝BC＝12，
∴AQ＝12﹣t，
∴y＝S四边形ABPQ＝
（BP+AQ）AE＝（2t+12﹣t）×3＝t+18（0＜t≤6）
（3）由（2）知，AE＝3，
∵BC＝12，
∴S四边形ABCD＝12×3＝36，
由（2）知，y＝S四边形ABPQ＝t+18（0＜t≤6），
∵四边形ABPQ的面积是四边形ABCD的面积的四分之三
∴t+18＝
×36，
∴t＝6；
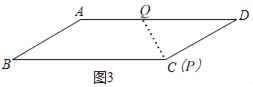
如图3，
当t＝6时，点P和点C重合，DQ＝6，
∵CD＝AB＝6，
∴DP＝DQ，
∴∠DQC＝∠DPQ，
∴∠D＝∠B＝30°，
∴∠DQP＝75°；
（4）①当AB＝BP时，BP＝6，
即2t＝6，t＝3；
②当AP＝BP时，如图2，
∵∠B＝30°，
过P作PM垂直于AB，垂足为点M，
∴BM＝3，BP＝2
∴2t＝2，
∴t＝
③当AB＝AP时，同（2）的方法得，BP＝6，
∴2t＝6，
∴t＝3
所以，当t＝3或或3时，△ABP为等腰三角形．
