题目内容
【题目】已知反比例函数![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A. 其图象分别位于第一、三象限
B. 当![]() 时,
时,![]() 随
随![]() 的增大而减小
的增大而减小
C. 若点![]() 在它的图象上,则点
在它的图象上,则点![]() 也在它的图象上
也在它的图象上
D. 若点![]() 都在该函数图象上,且
都在该函数图象上,且![]() ,则
,则![]()
【答案】C
【解析】
根据反比例函数图象上点的坐标特征、反比例函数的性质解答.
解:反比例比例系数![]() 的正负决定其图象所在象限,当
的正负决定其图象所在象限,当![]() 时图象在第一、三象限;当
时图象在第一、三象限;当![]() 时图象在二、四象限,由题可知
时图象在二、四象限,由题可知![]() ,所以A错误;
,所以A错误;
当![]() 时,反比例函数图象在各象限内
时,反比例函数图象在各象限内![]() 随
随![]() 的增大而减小;当
的增大而减小;当![]() 时,反比例函数图象在各象限内
时,反比例函数图象在各象限内![]() 随
随![]() 的增大而增大,由题可知
的增大而增大,由题可知![]() ,当
,当![]() 时,
时,![]() 随
随![]() 的增大而增大,所以B错误;
的增大而增大,所以B错误;
比例系数![]() :如果任意一点在反比例图象上,则该点横纵坐标值的乘积等于比例系数
:如果任意一点在反比例图象上,则该点横纵坐标值的乘积等于比例系数![]() ,因为点
,因为点![]() 在它的图象上,所以
在它的图象上,所以![]() ,又因为点
,又因为点![]() 的横纵坐标值的乘积
的横纵坐标值的乘积![]() ,所以点
,所以点![]() 也在函数图象上,故C正确
也在函数图象上,故C正确
当![]() 时,反比例函数图象在各象限内
时,反比例函数图象在各象限内![]() 随
随![]() 的增大而增大,由题可知
的增大而增大,由题可知![]() ,所以当
,所以当![]() 时,
时,![]() 随
随![]() 的增大而增大,而D选项中的
的增大而增大,而D选项中的![]() 并不确定是否在同一象限内,所以
并不确定是否在同一象限内,所以![]() 的大小不能粗糙的决定!所以D错误;
的大小不能粗糙的决定!所以D错误;
故选:C

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
【题目】在学校组织的“最美数学小报”的评比中,校团委给每个同学的作品打分,成绩分为![]() 四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,将八(1)班与八(2)班的成绩整理并绘制成如下统计图:
四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,将八(1)班与八(2)班的成绩整理并绘制成如下统计图:
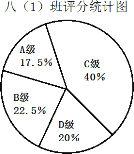

请你根据以上提供的信息解答下列问题:
(1)将表格补充完整.
平均数(分) | 中位数(分) | 众数(分) | |
八(1)班 | 83.75 | 80 | |
八(2)班 | 80 |
(2)若八(1)班有40人,且评分为B级及以上的同学有纪念奖章,请问该班共有几位同学得到奖章?