题目内容
【题目】(模型建立)
如图1,等腰直角三角形![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于点
于点![]() .
.

求证:![]() ;
;
(模型应用)
①已知直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,将直线
,将直线![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() 至直线
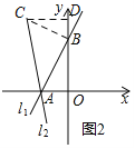
至直线![]() ,如图2,求直线
,如图2,求直线![]() 的函数表达式;
的函数表达式;

②如图3,在平面直角坐标系中,点![]() ,作
,作![]() 轴于点
轴于点![]() ,作
,作![]() 轴于点
轴于点![]() ,
,![]() 是线段
是线段![]() 上的一个动点,点
上的一个动点,点![]() 是直线
是直线![]() 上的动点且在第一象限内.问点
上的动点且在第一象限内.问点![]() 、
、![]() 、
、![]() 能否构成以点
能否构成以点![]() 为直角顶点的等腰直角三角形,若能,请直接写出此时点
为直角顶点的等腰直角三角形,若能,请直接写出此时点![]() 的坐标,若不能,请说明理由.
的坐标,若不能,请说明理由.

【答案】【模型建立】详见解析;【模型应用】①![]() ;②Q点坐标为(4,2)或(
;②Q点坐标为(4,2)或(![]() ,
,![]() ).
).
.
【解析】
模型建立:根据△ABC为等腰直角三角形,AD⊥ED,BE⊥ED,可判定△ACD≌△CBE;
模型应用:①过点B作BC⊥AB,交l2于C,过C作CD⊥y轴于D,根据△CBD≌△BAO,得出BD=AO=2,CD=OB=3,求得C(-3,5),最后运用待定系数法求直线l2的函数表达式;
②分两种情况考虑:如图3,∠AQP=90°,AQ=PQ,设Q点坐标为(a,2a-6),利用三角形全等得到a+6-(2a-6)=8,得a=4,易得Q点坐标;如图4,同理求出Q的坐标.
模型建立:证明:∵![]() ,
,![]()
∴![]() .
.
∵![]() ,∠ACB=90°.
,∠ACB=90°.
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
在![]() 与
与![]() 中,
中,
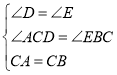 ,
,
∴![]() .
.
模型应用:
如图2,过点![]() 作
作![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() ,
,
∵![]() ,
,
∴![]() 为等腰直角三角形.
为等腰直角三角形.
由(1)可知:![]() ,
,
∴![]() ,
,![]() .
.
∵![]()
∴令![]() ,得
,得![]() ,∴
,∴![]() ,
,
令![]() ,得
,得![]() ,∴
,∴![]() .
.
∴![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
设![]() 的解析式为
的解析式为![]()
∴![]()
∴![]()
![]() 的解析式:
的解析式:![]() .
.
分以下两种情况:
如图3,当∠AQP=90°时,AQ=PQ,过点Q作EF⊥y轴,分别交y轴和直线BC于点E、F.
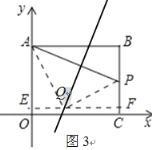
在△AQE和△QPF中,由(1)可得,△AQE≌△QPF(AAS),
AE=QF,设点Q的坐标为(a,2a-6),即6-(2a-6)=8-a,解得a=4.
此时点Q的坐标为(4,2).
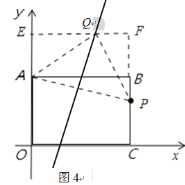
如图4:当∠AQP=90°时,AQ=PQ时,过点Q作EF⊥y轴,分别交y轴和直线BC于点E、F,设点Q的坐标为(a,2a-6),则AE=2a-12,FQ=8-a.
 ,
,
在△AQE和△QPF中,同理可得△AQE≌△QPF(AAS),
AE=QF,即2a-12=8-a,解得a=![]() .
.
此时点Q的坐标为(![]() ,
,![]() ).
).
综上所述:A、P、Q可以构成以点Q为直角顶点的等腰直角三角形,点Q的坐标为 (4,2)或(![]() ,
,![]() ).
).

 阅读快车系列答案
阅读快车系列答案





