Question

【题目】如图，在等边三角形ABC中，点D，E分别在边BC，AC上，DE∥AB，过点E作EF⊥DE，交BC的延长线于点F．

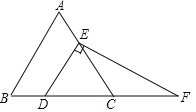
（1）求∠F的度数；

（2）若CD=2，求DF的长．

Answer 1

【答案】(1)、30°；(2)、4.

【解析】

试题分析：(1)、根据等边三角形的性质得出∠B=60°，根据DE∥AB得出∠EDC=60°，根据垂直得出∠DEF=90°，根据三角形内角和定理可得∠F的度数；(2)、根据∠ACB=∠EDC=60°得出△EDC为等边三角形，则ED=DC=2，根据∠DEF=90°，∠F=30°得出DF=2DE=4.

试题解析：(1)、∵△ABC是等边三角形， ∴∠B=60°， ∵DE∥AB， ∴∠EDC=∠B=60°

∵EF⊥DE， ∴∠DEF=90°， ∴∠F=90°﹣∠EDC=30°

(2)、∵∠ACB=60°，∠EDC=60°， ∴△EDC是等边三角形．∴ED=DC=2，

∵∠DEF=90°，∠F=30° ∴DF=2DE=4．