��Ŀ����
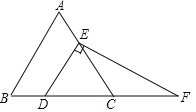
����Ŀ�����壺��ͼ��������ABC�У�CD��AB���ϵ����ߣ���ô��ACD����BCD�����Ѻ���������������S��ACD=S��BCD��Ӧ�ã���ͼ�����ھ���ABCD�У�AB=4��BC=6����E��AD�ϣ���F��BC�ϣ�AE=BF��AF��BE���ڵ�O��
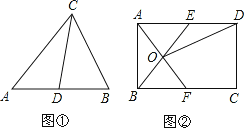
��1����֤����AOB����AOE�����Ѻ�����������
��2������OD������AOE����DOE�����Ѻ��������������ı���CDOF�������
���𰸡���1��֤������������2��12.
��������
�����������1������һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ��õ��ı���ABFE��ƽ���ı��Σ�Ȼ�����ƽ���ı��ε�����֤��OE=OB������֤����AOE����AOB���Ѻ������Σ�
��2����AOE����DOE�����Ѻ��������������ɵõ�E��AD���е㣬����������ABE����ABF�����������S�ı���CDOF=S����ABCD-2S��ABF������⣮
�����������1������EF��
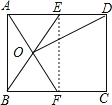
���ı���ABCD�Ǿ��Σ�
��AD��BC��
��AE=BF��
���ı���ABFE��ƽ���ı��Σ�
��OE=OB��
���AOE����AOB���Ѻ������Σ�
��2���ߡ�AOE����DOE���Ѻ������Σ�
��S��AOE=S��DOE��AE=ED=![]() AD=3��
AD=3��
�ߡ�AOB����AOE���Ѻ������Σ�
��S��AOB=S��AOE��
�ߡ�AOE�ա�FOB��
��S��AOE=S��FOB��
��S��AOD=S��ABF��
��S�ı���CDOF=S����ABCD-2S��ABF=4��6-2��![]() ��4��3=12��
��4��3=12��