题目内容
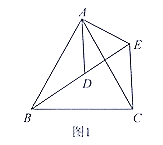
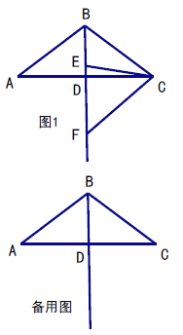
【题目】如图,在四边形ABCD中,AB∥CD,点E在AB上,AB=DC=DE, AD⊥AB,BC⊥AB,CF⊥DE,垂足分别为点A,B,F,AD=BC=6,EB=2.
(1)求证:CF=CB;
(2)求△DEC的面积S的值;
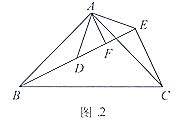
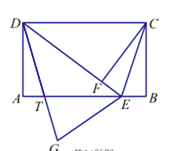
(3)若将△DEC沿着DE翻折得到△DEG,DG交AB于点T,试判断线段DT与CE的长度是否相等:并说明理由.
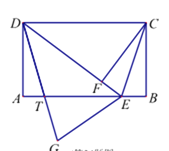
【答案】(1)证明见解析;(2)30;(3)不相等,理由见解析.
【解析】
(1)根据AB∥CD,可得∠CDE=∠DEA,由AD⊥AB,CF⊥DE,可得∠A=∠CFD=90°,然后根据AAS定理证明△DCF≌△EDA,从而得到CF=DA,问题得解;(2)利用CF=CB,CE=CE,根据HL定理证明Rt△CFE≌Rt△CBE,得到EF=EB=2,设DE=DC=x,利用勾股定理列方程求DE的长,从而求出三角形面积;(3)利用勾股定理求出CE的长,然后根据折叠的性质和平行线的性质,可得DT=TE,设DT=TE=y,在Rt△DAT中,列方程求DT的长,从而求证问题.
解:(1)∵AB∥CD
∴∠CDE=∠DEA
∵AD⊥AB,CF⊥DE
∴∠A=∠CFD=90°
又∵DC=DE
∴△DCF≌△EDA
∴CF=DA
∵AD=BC
∴CF=CB
(2)∵BC⊥AB,CF⊥DE
∴∠B=∠CFE=90°
又∵CF=CB,CE=CE
∴Rt△CFE≌Rt△CBE(HL)
∴∠CFD=∠B=90°,CF=BC=6,EF=EB=2
设DE=DC=x,则DF=x-2
由题意,在Rt△DFC中,![]()
解得:x=10
∴![]()
(3)由题意可知,在Rt△BCE中,![]()
由折叠性质可知,∠TDE=∠CDE
∵AB∥CD
∴∠CDE=∠DEA
∴∠TDE=∠DEA
∴DT=TE
设DT=TE=y,则AT=10-2-y=8-y
在Rt△DAT中,![]()
解得:![]()
∴DT与CE的长度不相等

 阅读快车系列答案
阅读快车系列答案