题目内容
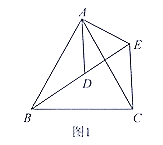
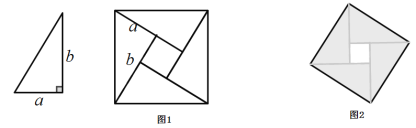
【题目】我国古代数学家赵爽曾用图1证明了勾股定理,这个图形被称为“弦图”.2002年在北京召开的国际数学家大会(ICM 2002)的会标(图2),其图案正是由“弦图”演变而来.“弦图”是由4个全等的直角三角形与一个小正方形组成,恰好拼成一个大正方形请你根据图1解答下列问题:
(1)叙述勾股定理(用文字及符号语言叙述);
(2)证明勾股定理;
(3)若大正方形的面积是![]() ,小正方形的面积是
,小正方形的面积是![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)证明见解析;(3)25.
【解析】
(1)直接叙述勾股定理的内容,并用字母表明三边关系;
(2)利用大正方形面积、小正方形面积和4个直角三角形的面积和之间的关系列式整理即可证明;
(3)将原式利用完全平方公式展开,由勾股定理的内容可得出![]() 为大正方形面积和4个直角三角形的面积和,根据已知条件即可求得.
为大正方形面积和4个直角三角形的面积和,根据已知条件即可求得.
解:(1)勾股定理:直角三角形两直角边的平方和等于斜边的平方.
在直角三角形中,两条直角边分别为 a、b,斜边为 c,a2+b2= c2.
(2)∵ S大正方形=c2,S小正方形=(b-a)2,4 SRt△=4×![]() ab=2ab,
ab=2ab,
∴ c2=2ab+(b-a)2=2ab+b2-2ab+a2=a2+b2,
即 a2+b2= c2.
(3)∵ 4 SRt△= S大正方形- S小正方形=13-1=12,
∴ 2ab=12.
∴ (a+b)2= a2+b2+2ab=c2+2ab=13+12=25.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目