题目内容
某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)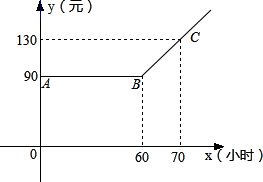 的关系如图所示,其中AB是线段,且AB∥x轴,BC是射线
的关系如图所示,其中AB是线段,且AB∥x轴,BC是射线(1)若小李10月份上网20小时,他应付多少元的上网费?
(2)当x≥60时,求y与x之间的函数关系式;
(3)若小李11月份的上网费用为210元,则他在11月份的上网时间是多少小时?
分析:根据图象可知:每月上网60小时以内收费90元;超过60小时按超过时间多少收费.
(1)20<60,故付费90元;
(2)根据B点和C点坐标,用待定系数法求解析式;
(3)求y=210时,x的值即可.
(1)20<60,故付费90元;
(2)根据B点和C点坐标,用待定系数法求解析式;
(3)求y=210时,x的值即可.
解答:解:(1)根据图象可知:每月上网60小时以内收费90元.所以上网20小时,他应付90元的上网费;
(2)设y=kx+b.
∵B(60,90),C(70,130),
∴
.
解之得
.
∴y=4x-150.(x≥60);
(3)当y=210时,即 4x-150=210.
解得 x=90.
答:若小李11月份的上网费用为210元,则他在11月份的上网时间是90小时.
(2)设y=kx+b.
∵B(60,90),C(70,130),
∴
|
解之得
|
∴y=4x-150.(x≥60);
(3)当y=210时,即 4x-150=210.
解得 x=90.
答:若小李11月份的上网费用为210元,则他在11月份的上网时间是90小时.
点评:此题考查一次函数的应用,注意分段函数中自变量的取值范围.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
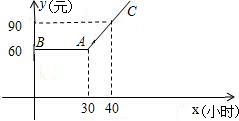 中BA是线段,且BA∥x轴,AC是射线.
中BA是线段,且BA∥x轴,AC是射线.