题目内容
如图,已知AB是圆O的直径,BC是圆O的弦,弦ED⊥AB于点F,交BC于点G,过点C作圆O的切线与ED的延长线交于点P.

(1)求证:PC=PG;
(2)点C在劣弧AD上运动时,其他条件不变,若点G是BC的中点,试探究CG、BF、BO三者之间的数量关系,并写出证明过程;
(3)在满足(2)的条件下,已知圆为O的半径为5,若点O到BC的距离为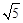 时,求弦ED的长.
时,求弦ED的长.
解:(1)证明:如图,连接OC,
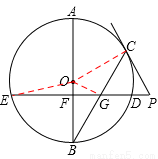
∵PC为⊙O的切线,∴OC⊥PC。∴∠OCG+∠PCG=90°。
∵ED⊥AB,∴∠B+∠BGF=90°。
∵OB=OC,∴∠B=∠OCG。∴∠PCG=∠BGF。
又∵∠BGF=∠PGC,∴∠PGC=∠PCG。
∴PC=PG。
(2)CG、BF、BO三者之间的数量关系为CG2=BO•BF。理由如下:
如图,连接OG,
∵点G是BC的中点,∴OG⊥BC,BG=CG。∴∠OGB=90°。
∵∠OBG=∠GBF,∴Rt△BOG∽Rt△BGF。∴BG:BF=BO:BG。
∴BG2=BO•BF。∴CG2=BO•BF。
(3)如图,连接OE,
由(2)得BG⊥BC,∴OG= 。
。
在Rt△OBG中,OB=5,∴ 。
。
由(2)得BG2=BO•BF,∴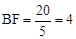 。∴OF=1。
。∴OF=1。
在Rt△OEF中,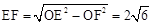 。
。
∵AB⊥ED,∴EF=DF。
∴DE=2EF=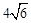 。
。
【解析】
试题分析:(1)连接OC,根据切线的性质得OC⊥PC,则∠OCG+∠PCG=90°,由ED⊥AB得∠B+∠BGF=90°,而∠B=∠OCG,所以∠PCG=∠BGF,根据对顶角相等得∠BGF=∠PGC,于是∠PGC=∠PCG,所以PC=PG。
(2)连接OG,由点G是BC的中点,根据垂径定理的推论得OG⊥BC,BG=CG,易证得Rt△BOG∽Rt△BGF,则BG:BF=BO:BG,即BG2=BO•BF,把BG用CG代换得到CG2=BO•BF。
(3)连接OE,OG=OG= ,在Rt△OBG中,利用勾股定理计算出BG=2
,在Rt△OBG中,利用勾股定理计算出BG=2 ,再利用BG2=BO•BF可计算出BF,从而得到OF=1,在Rt△OEF中,根据勾股定理计算出EF=2
,再利用BG2=BO•BF可计算出BF,从而得到OF=1,在Rt△OEF中,根据勾股定理计算出EF=2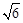 ,由于AB⊥ED,根据垂径定理可得EF=DF,于是有DE=2EF=4
,由于AB⊥ED,根据垂径定理可得EF=DF,于是有DE=2EF=4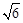 。
。

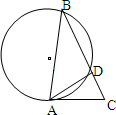 9、如图,已知AB是圆O的弦,AC是圆O的切线,∠BAC的平分线交圆O于D,连BD并延长交AC于点C,若∠DAC=40°,则∠B=
9、如图,已知AB是圆O的弦,AC是圆O的切线,∠BAC的平分线交圆O于D,连BD并延长交AC于点C,若∠DAC=40°,则∠B=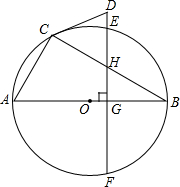 如图:已知AB是圆O的直径,BC是圆O的弦,圆O的割线DEF垂直于AB于点G,交BC于点H,DC=DH.
如图:已知AB是圆O的直径,BC是圆O的弦,圆O的割线DEF垂直于AB于点G,交BC于点H,DC=DH.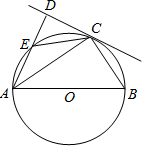 如图,已知AB是圆O的直径,DC是圆O的切线,点C是切点,AD⊥DC垂足为D,且与圆O相交于点E.
如图,已知AB是圆O的直径,DC是圆O的切线,点C是切点,AD⊥DC垂足为D,且与圆O相交于点E.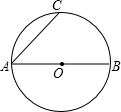 (1998•上海)如图,已知AB是圆O的直径,AC是弦,AB=2,AC=
(1998•上海)如图,已知AB是圆O的直径,AC是弦,AB=2,AC=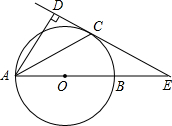 如图,已知AB是圆O的直径,∠DAB的平分线AC交圆O与点C,作CD⊥AD,垂足为点D,直线CD与AB的延长线交于点E.
如图,已知AB是圆O的直径,∠DAB的平分线AC交圆O与点C,作CD⊥AD,垂足为点D,直线CD与AB的延长线交于点E.