Question

（1998•上海）如图，已知AB是圆O的直径，AC是弦，AB=2，AC=

2

，在图中画出弦AD，使AD=1，并求出∠CAD的度数．

Answer 1

分析：根据题意画出两个图形，过O作OE⊥AD于E，作OF⊥AC于F，求出AE、AF，根据三角函数值求出∠EAO和∠FAO，即可求出答案．

解答：解：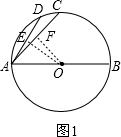
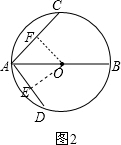
分为两种情况：①如图1，过O作OE⊥AD于E，作OF⊥AC于F，
由垂径定理得：AE=

1

2

AD=

1

2

，AF=

1

2

AC=

1

2

2

，
∵OA=

1

2

AB=1，
在△AEO和△AFO中，cos∠EAO=

AE

AO

=

1

2

，cos∠FAO=

AF

AO

=

2

2

，
∴∠EAO=60°，∠FAO=45°，
∴∠DAC=∠DAO-∠CAO=60°-45°=15°；
②如图2，∠DAC=60°+45°=105°．

点评：本题考查了垂径定理，特殊角的三角函数值等知识点的应用．