题目内容
【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CF,垂足为F.
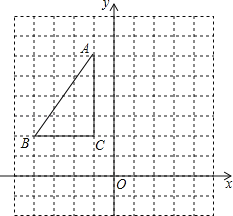
(1)若AC=10,求四边形ABCD的面积;
(2)求证:AC平分∠ECF;
(3)求证:CE=2AF.
【答案】(1)解:∵∠BAD=∠CAE=90°,
∴∠BAC+∠CAD=∠EAD+∠CAD
∴∠BAC=∠EAD,
在△ABC和△ADE中, ,
,
∴△ABC≌△ADE(SAS),
∵S四边形ABCD=S△ABC+S△ACD ,
∴![]() ;
;
(2)证明:∵△ACE是等腰直角三角形,
∴∠ACE=∠AEC=45°,
由△ABC≌△ADE得:
∠ACB=∠AEC=45°,
∴∠ACB=∠ACE,
∴AC平分∠ECF;
(3)证明:过点A作AG⊥CG,垂足为点G,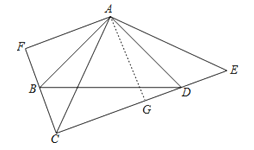
∵AC平分∠ECF,AF⊥CB,
∴AF=AG,
又∵AC=AE,
∴∠CAG=∠EAG=45°,
∴∠CAG=∠EAG=∠ACE=∠AEC=45°,
∴CG=AG=GE,
∴CE=2AG,
∴CE=2AF.
【解析】(1)求出∠BAC=∠EAD,根据SAS推出△ABC≌△ADE,推出四边形ABCD的面积=三角形ACE的面积,即可得出答案;
(2)根据等腰直角三角形的性质得出∠ACE=∠AEC=45°,△ABC≌△ADE求出∠ACB=∠AEC=45°,推出∠ACB=∠ACE即可;
(3)过点A作AG⊥CG,垂足为点G,求出AF=AG,求出CG=AG=GE,即可得出答案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目