Question

【题目】如图，在矩形OABC纸片中，OA=7，OC=5，D为BC边上动点，将△OCD沿OD折叠，当点C的对应点落在直线AF上时，记为点E，若此时连接CE，同时OA＝OF，,则△OCE面积为__．

Answer 1

【答案】或10.

【解析】试题解析：根据题意，画出平面直角坐标系为：

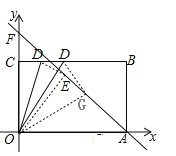
∵OA=OF

∴AF所在直线解析式为：y=-x+7

∵点E在直线l：y=-x+7上，
∴设点E的坐标为（x，-x+7），
∵OE=OC=5，
∴，
解得：x1=3，x2=4，
∴点E的坐标为（3，4），点G的坐标为（4，3）．

∵BC∥x轴，且OC=5，

∴设点D的坐标为（m，5）（m＞0），则CD=m．

∵ED=CD或GD=CD，

∴或，

解得：m=或m=．

即CD的长为或.

当CD=时,连接CE,得OD垂直平分CE,交OD于H ,如图,

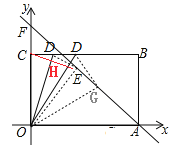
由勾股定理可求出OD=

根据面积相等可求出CH=，OH=

∴SΔOCH=

∴SΔOCE=

同理可求：SΔOCG=10.