题目内容
 如下图所示,在△ABC中,∠A=40°,∠B=90°,AC的垂直平分线MN分别与AB、AC交于点D、E,求∠BCD的度数.
如下图所示,在△ABC中,∠A=40°,∠B=90°,AC的垂直平分线MN分别与AB、AC交于点D、E,求∠BCD的度数.
分析:利用MN是AC的垂直平分线,可得AE=AC,进而利用两个三角形全等的判定方法“两边和它们的夹角对应相等的两个三角形相等”可证△AED≌△DEC,进而可得∠DCA=∠A=40°,又从△ABC中,可得∠ACB=50°,可得出∠BCD=10°.
解答:解:∵∠B=90°,∠A=40°,∴∠ACB=50°,
∵MN是线段AC的垂直平分线.
∴AE=CE.
在△ADE和△CDE中,
.
.
∴△ADE≌△CDE(SAS)
∴∠DCA=∠A=40°
∴∠BCD=∠ACB-∠DCA
=50°-40°
=10°.
∵MN是线段AC的垂直平分线.
∴AE=CE.
在△ADE和△CDE中,
.
|
∴△ADE≌△CDE(SAS)
∴∠DCA=∠A=40°
∴∠BCD=∠ACB-∠DCA
=50°-40°
=10°.
点评:掌握并理解垂直平分线的定义.并充分利用两个三角形全等后对应的两角相等的性质来解决问题.

练习册系列答案
相关题目
 如下图所示,在△ABC中,AB=AC,BC=6,点E、F是中线AD上的两点,且AD=4,则图中阴影部分的面积为( )
如下图所示,在△ABC中,AB=AC,BC=6,点E、F是中线AD上的两点,且AD=4,则图中阴影部分的面积为( )| A、6 | B、12 | C、24 | D、3 |
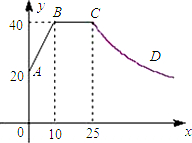 心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如下图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如下图所示(其中AB、BC分别为线段,CD为双曲线的一部分): 11、证明:如下图所示,在四边形ABCD中,AB+BD≤AC+CD,求证:AB<AC.
11、证明:如下图所示,在四边形ABCD中,AB+BD≤AC+CD,求证:AB<AC. 如下图所示,在等边△ABC中,AD⊥BC,BD=3,则AB=
如下图所示,在等边△ABC中,AD⊥BC,BD=3,则AB=