题目内容
【题目】如图①,△ABC是等边三角形,点P是BC上一动点(点P与点B、C不重合),过点P作PM∥AC交AB于M,PN∥AB交AC于N,连接BN、CM.

(1)求证:PM+PN=BC;
(2)在点P的位置变化过程中,BN=CM是否成立?试证明你的结论;
(3)如图②,作ND∥BC交AB于D,则图②成轴对称图形,类似地,请你在图③中添加一条或几条线段,使图③成轴对称图形(画出一种情形即可).
【答案】(1)见解析;(2)结论成立,理由见解析;(3)见解析
【解析】
(1)先证明△BMP,△CNP是等边三角形,再证明△BPN≌△MPC,从而PM=PB,PN=PC,可得PM+PN=BC;
(2)BN=CM总成立,由(1)知△BPN≌△MPC,根据全等三角形的性质可得结论;
(3)作ND∥BC交AB于N,作ME∥BC交AC于M,作EF∥AB交BC于F,连接DF即可.
(1)证明:∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠ACB=60°,
∵PM∥AC,PN∥AB,
∴∠BPM=∠ACB=60°,∠CPN=∠ABC=60°,
∴△BMP,△CNP是等边三角形,
∴∠BPM=∠CPN=60°,PN=PC,PN=PC,
∴∠BPN=∠MPC,
∴△BPN≌△MPC,
∴PM=PB,PN=PC,
∵BP+PC=BC,
∴PM+PN=BC;
(2)BN=CM总成立,理由:
由(1)知△BPN≌△MPC,
∴BN=CM;
(3)解:如图③即为所求.
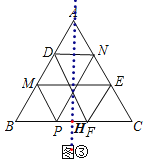
作ND∥BC交AB于N,作ME∥BC交AC于M,作EF∥AB交BC于F,连接DF,作直线AH⊥BC交BC于H,
同(1)可证△AND,△AME,△BPM,△CEF都是等边三角形,
∴D与N,M与E,B与C关于AH对称.
∴BM=CE,
∴BM=CF,
∴P与F关于AH对称,
∴所做图形是轴对称图形.