题目内容
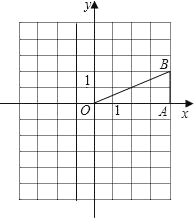
【题目】如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.
(1)画出将△OAB绕原点顺时针旋转90°后所得的△OA1B1,并写出点A1、B1的坐标;
(2)画出△OAB关于原点O的中心对称图形△OA2B2,并写出点A2、B2的坐标.
【答案】(1)A1、B1的坐标分别为(﹣2,4)(﹣2,0);
(2)点B2、A2的坐标分别为(﹣4,﹣2)、(﹣4,0).
【解析】
试题(1)将点B绕原点逆时针方向旋转90°可理解为把Rt△OAB绕原点逆时针方向旋转90°,画图后即可得到A1、B1点坐标;
(2)根据关于原点对称的坐标特征求解.
试题解析:(1)如图,
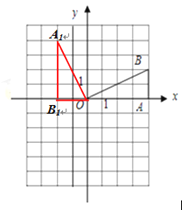
A1、B1的坐标分别为(﹣2,4)(﹣2,0);
(2)如图:

点B2、A2的坐标分别为(﹣4,﹣2)、(﹣4,0).

练习册系列答案
相关题目