Question

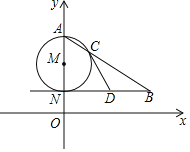
【题目】如图，正方形ABCD的边长为2，点E在边AD上(不与A，D重合)，点F在边CD上，且∠EBF=45°，若△ABE的外接圆⊙O与CD边相切．

(1)求⊙O的半径长；

(2)求△BEF的面积．

Answer 1

【答案】（1）；（2）.

【解析】

（1）将△BCF绕点B逆时针旋转90°到△BAP，过点B作BQ⊥EF，设⊙O与CD相切于点M，连接OM，延长MO交AB于点N，由已知得出△BPE≌△BFE，进而得出△AEB≌△QEB，利用中位线出AE的长，由勾股定理求出BE，即可得出半径；
（2）由C△EFD=4，利用勾股定理得出DF的长，即可求出△BEF的面积．

解：（1）将△BCF绕点B逆时针旋转90°到△BAP，过点B作BQ⊥EF，设⊙O与CD相切于点M，连接OM，延长MO交AB于点N，如图所示：

在△BPE与△BFE中， ，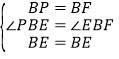

∴△BPE≌△BFE（SAS），

∴∠AEB=∠BEQ，PE=EF，

在△AEB和△QEB中， ，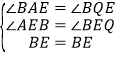

∴△AEB≌△QEB（AAS），

∴BQ=AB=2，

由PE=EF可知，

C△EFD=ED+DF+EF=ED+DF+PE=ED+DF+PA+AE=ED+AE+DF+FC=4，

设AE=a，则DE=2﹣a，BE= ，

∵O为BE中点，且MN∥AD，

∴ON=AE= ，

∴OM=2﹣，

又BE=2OM，

∴=4﹣a，解得a= ，

∴ED=，BE= = ，

∴⊙O的半径长=BE= ；

（2）∵C△EFD=4，设DF=b，

∴EF=4﹣b﹣=﹣b，

在Rt△EDF中，（）2+b2=（﹣b）2，

解得b= ，

∴EF=﹣= ，

∴S△BEF=××2=．