题目内容
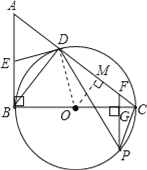
【题目】如图,已知AB是⊙O的切线,BC为⊙O的直径,AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F
(1)求证:ED是⊙O的切线;
(2)求证:△CFP∽△CPD;
(3)如果CF=1,CP=2,sinA=![]() ,求O到DC的距离.
,求O到DC的距离.

【答案】(1)证明见解析;(2)证明见解析;(3)O到DC的距离为![]() .
.
【解析】试题分析:(1)连接OD,证OD⊥DE即可.易证∠ADB=90°,又点E为AB的中点,得DE=EB.根据等腰三角形性质可证∠ODE=∠OBE=90°,得证;
(2)可证∠A=∠DBC,所以要求BC需先求DC.结合已知条件,证明△PDC与△FPC相似.
(3)根据△PCF∽△DCP,得出CD的长度,进而求出O到DC的距离即可.
试题解析:(1)连接OD.
∵BC为直径,
∴△BDC为直角三角形.
在Rt△ADB中,E为AB中点,
∴BE=DE,
∴∠EBD=∠EDB.
又∵OB=OD,∴∠OBD=∠ODB,
∵∠OBD+∠ABD=90°,∴∠ODB+∠EDB=90°.
∴ED是⊙O的切线.
(2)∵PF⊥BC,
∴∠FPC=90°﹣∠BCP(直角三角形的两个锐角互余).
∵∠PDC=90°﹣∠PDB(直径所对的圆周角是直角),∠PDB=∠BCP(同弧所对的圆周角相等),
∴∠FPC=∠PDC(等量代换).
又∵∠PCF是公共角,
∴△PCF∽△DCP.
(3)过点O作OM⊥CD于点M,
∵△PCF∽△DCP,
∴PC2=CFCD(相似三角形的对应边成比例).
∵CF=1,CP=2,
∴CD=4.
可知sin∠DBC=sinA=sin∠MOC=![]() ,
,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴直径BC=5,
∴![]() =
=![]() ,
,
∴MC=2,
∴MO=![]() ,
,
∴O到DC的距离为![]() .
.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
