题目内容
已知△ABC的三边长分别为9cm、14cm、13cm,分别以A、B、C三点为圆心作圆,使所作的三个圆两两外切,则其中最大圆的半径
为
- A.8cm
- B.9cm
- C.10cm
- D.11cm
B
分析:画出图形:⊙A、⊙B、⊙C两两外切,切点分别为D、F、E,设⊙A、⊙B、⊙C的半径分别为acm,bcm,dcm,根据相切两圆的连心线必过切点得出AB过D,BC过F,AC过E,根据相切两圆的性质得出方程组,求出方程组的解即可.
解答:
解:如图所示:⊙A、⊙B、⊙C两两外切,切点分别为D、F、E,
设⊙A、⊙B、⊙C的半径分别为acm,bcm,dcm,
根据相切两圆的连心线必过切点得出AB过D,BC过F,AC过E,
∵AB=9cm,BC=13cm,AC=14cm,
∴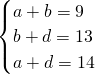 ,
,
解得:a=5,b=4,d=9,
即最大圆的半径是9cm,
故选B.
点评:本题考查了相切两圆的性质和解三元一次方程组,注意:相切两圆的连心线必过切点.
分析:画出图形:⊙A、⊙B、⊙C两两外切,切点分别为D、F、E,设⊙A、⊙B、⊙C的半径分别为acm,bcm,dcm,根据相切两圆的连心线必过切点得出AB过D,BC过F,AC过E,根据相切两圆的性质得出方程组,求出方程组的解即可.
解答:

解:如图所示:⊙A、⊙B、⊙C两两外切,切点分别为D、F、E,
设⊙A、⊙B、⊙C的半径分别为acm,bcm,dcm,
根据相切两圆的连心线必过切点得出AB过D,BC过F,AC过E,
∵AB=9cm,BC=13cm,AC=14cm,
∴
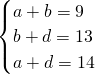 ,
,解得:a=5,b=4,d=9,
即最大圆的半径是9cm,
故选B.
点评:本题考查了相切两圆的性质和解三元一次方程组,注意:相切两圆的连心线必过切点.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目