题目内容
【题目】如图,抛物线经过A(﹣1,0),B(3,0),C(0, ![]() )三点.
)三点.

(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
【答案】(1)抛物线的解析式为: ![]() ;
;
(2)P(1,1);
(3)存在,点N的坐标为(2, ![]() ),(
),(![]() ,
, ![]() ),(
),(![]() ,
, ![]() ).
).
【解析】【试题分析】
(1)设抛物线的解析式为y=ax2+bx+c(a≠0),因为A(﹣1,0),B(5,0),C(0, ![]() )三点在抛物线上,则构造三元方程组,得
)三点在抛物线上,则构造三元方程组,得 ,解得
,解得 .即抛物线的解析式为:
.即抛物线的解析式为: ![]() ;
;
(2)如图1,根据抛物线的解析式为![]() ,得其对称轴为直线:
,得其对称轴为直线:  ,连接BC,设直线BC的解析式为
,连接BC,设直线BC的解析式为![]() ,
,
根据B、C两点,得方程组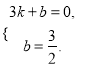 解得
解得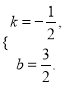
即直线BC的解析式为![]() ,当x=1时,
,当x=1时, ![]() .∴P(1,1);
.∴P(1,1);
(3)存在.A(﹣1,0),C(0, ![]() ),M(m,0),
),M(m,0), ![]() ,根据相对的两个点的中点坐标重合.
,根据相对的两个点的中点坐标重合.
若A、C相对,则 ,解得n=2, ∴N1(2,
,解得n=2, ∴N1(2, ![]() );
);
若A、M相对,则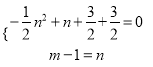 ,解得n=
,解得n=![]() ∴N2(
∴N2(![]() ,
, ![]() ),N3(
),N3(![]() ,
, ![]() ).;
).;
若A、N相对,则 ,解得n=2,(舍去);
,解得n=2,(舍去);
综上所述,点N的坐标为(2, ![]() ),(
),(![]() ,
, ![]() ),(
),(![]() ,
, ![]() ).
).
【试题解析】
(1)设抛物线的解析式为y=ax2+bx+c(a≠0),
∵A(﹣1,0),B(5,0),C(0, ![]() )三点在抛物线上,
)三点在抛物线上,
∴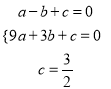 ,解得
,解得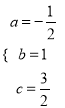 .
.
∴抛物线的解析式为: ![]() ;
;
(2)∵抛物线的解析式为![]() ,
,
∴其对称轴为直线:  .
.
连接BC,设直线BC的解析式为![]() ,
,
∵B(3,0),C(0, ![]() ),∴
),∴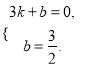 解得
解得
∴直线BC的解析式为![]()
当x=1时, ![]() .∴P(1,1);
.∴P(1,1);
(3)存在.
存在.A(﹣1,0),C(0, ![]() ),M(m,0),
),M(m,0), ![]()
若A、C相对,则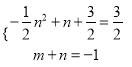 ,解得n=2, ∴N1(2,
,解得n=2, ∴N1(2, ![]() );
);
若A、M相对,则 ,解得n=
,解得n=![]() ∴N2(
∴N2(![]() ,
, ![]() ),N3(
),N3(![]() ,
, ![]() ).;
).;
若A、N相对,则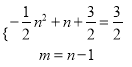 ,解得n=2,(舍去);
,解得n=2,(舍去);
综上所述,点N的坐标为(2, ![]() ),(
),(![]() ,
, ![]() ),(
),(![]() ,
, ![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案