题目内容
【题目】如图,AC是⊙O的直径,点B在⊙O上,∠ACB=30°.

(1)利用尺规作∠ABC的平分线BD,交AC于点E,交⊙O于点D,连接CD(保留作图痕迹,不写作法)
(2)在(1)所作的图形中,求AB与CD的比值.
【答案】(1)画图见解析;
(2)![]() .
.
【解析】【试题分析】(1)尺规作图,作一个角的平分线;(2)如图2,连接OD,设⊙O的半径为r,因为AC是⊙O的直径,∴∠ABC=90°..
在Rt△ACB中,∠ACB=30°,根据30度的直角边是斜边的一半,AB=![]() AC=r.
AC=r.
由于BD是∠ABC的平分线,根据角平分线的定义得,∠ABD=∠CBD=45° .
根据同弧所对的圆周角是圆心角的一半,得∠DOC=2∠CBD =90°
在Rt△ODC中,DC=![]() =
=![]() r.则
r.则![]() .
.
【试题解析】
(1)如图所示;

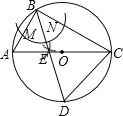
(2)如图2,连接OD,设⊙O的半径为r,
∵AC是⊙O的直径,∴∠ABC=90°..
在Rt△ACB中,∠ACB=30°,
∴AB=![]() AC=r.
AC=r.
∵BD是∠ABC的平分线,∴∠ABD=∠CBD=45° .
∴∠DOC=2∠CBD =90°
在Rt△ODC中,DC=![]() =
=![]() r.
r.
∴![]() .
.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目

