题目内容
把直角三角形两条直角边同时扩大为原来的2倍,则其斜边扩大为原来的( )
| A、2倍 | ||
| B、4倍 | ||
C、
| ||
| D、不能确定 |
考点:勾股定理
专题:
分析:根据勾股定理求出扩大后斜边的长度,与原斜边长度比较即可得出答案.
解答:解:设一直角三角形直角边为a、b,斜边为c,则a2+b2=c2;
扩大2倍后,直角三角形直角边为2a、2b,则根据勾股定理知斜边为
=2c.
即直角三角形的两条直角边同时扩大到原来的2倍,则斜边扩大为原来的2倍.
故选:A.
扩大2倍后,直角三角形直角边为2a、2b,则根据勾股定理知斜边为
| (2a)2+(2b)2 |
即直角三角形的两条直角边同时扩大到原来的2倍,则斜边扩大为原来的2倍.
故选:A.
点评:此题考查了勾股定理的知识,属于基础题,解答本题关键是利用勾股定理求出扩大后斜边的长度,难度一般.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
已知m、n是两个连续自然数(m<n),且q=mn,设p=
+
,则p( )
| q+n |
| q-n |
| A、总是奇数 |
| B、总是偶数 |
| C、有时是奇数,有时是偶数 |
| D、有时是有理数,有时是无理数 |
在Rt△ABC中,a,b,c为△ABC三边长,则下列关系正确的是( )
| A、a2+b2=c2 |
| B、a2+c2=b2 |
| C、b2+c2=a2 |
| D、以上关系都有可能 |
下列计算正确的有( )
(1)
+
=
;(2)2+
=5
;(3)3
-
=
;(4)
=
+
=2+5=7.
(1)
| 3 |
| 4 |
| 7 |
| 5 |
| 5 |
| a |
| b |
| a-b |
| ||||
| 3 |
| 4 |
| 25 |
| A、0个 | B、1个 | C、2个 | D、3个 |
 将一个矩形的纸对折两次,沿图中虚线将一角剪掉再打开后,得到的图形为( )
将一个矩形的纸对折两次,沿图中虚线将一角剪掉再打开后,得到的图形为( )A、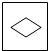 |
B、 |
C、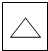 |
D、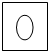 |
下列四个条件中,能判定四边形是平行四边形的是( )
| A、一组对边平行,另一组对边相等 |
| B、两条对角线互相垂直 |
| C、两条对角线相等 |
| D、一组对边平行,一组对角相等 |
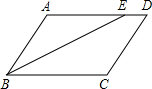 如图,?ABCD中,BE平分∠ABC且交边AD于点E,如果AB=6cm,BC=10cm,则线段DE=
如图,?ABCD中,BE平分∠ABC且交边AD于点E,如果AB=6cm,BC=10cm,则线段DE= 如图是两个可以自由转动的转盘,转盘均被等分成三个扇形,并分别标上1,2,3和6,7,8这6个数字.如果同时转动两个转盘各一次(指针落在等分线上重转),则转盘停止后指针指向的数字之和为偶数的概率是
如图是两个可以自由转动的转盘,转盘均被等分成三个扇形,并分别标上1,2,3和6,7,8这6个数字.如果同时转动两个转盘各一次(指针落在等分线上重转),则转盘停止后指针指向的数字之和为偶数的概率是