题目内容
【题目】如图,△ABC为等边三角形,D是△ABC内一点,若将△ABD经过一次逆时针旋转后到△ACP的位置,则旋转中心是 ,旋转角等于 °,△ADP是 三角形.
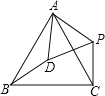
【答案】A,60,等边.
【解析】
试题分析:观察图形,找旋转中心,旋转方向,旋转角;由旋转角是60°,对应点到旋转中心的距离AD与AP相等,可证△ADP为等边三角形.
解:根据题意分析可得:图中旋转中心是点A;
旋转角度是即∠DAP的大小,
∵将△ABD经过一次逆时针旋转后到△ACP的位置,
∴∠BAD=∠CAP,
∵∠BAC=∠BAD+∠DAC=60°,
∴∠PAC+∠CAD=60°
∴∠DAP=60°;
故旋转角度60度.
根据旋转的性质;可得AD=AP,且∠DAP=60°;故△ADP为等边三角形.
故答案为:A,60,等边.

练习册系列答案
相关题目