题目内容
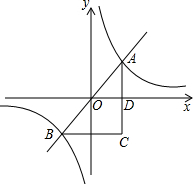 如图,正比例函数y=2x与反比例函数y=
如图,正比例函数y=2x与反比例函数y=| 5 |
| x |
10
10
,周长是3
+5
| 10 |
| 2 |
3
+5
.| 10 |
| 2 |
分析:将两函数解析式联立组成方程组,求出方程组的解得到两交点A与B的坐标,又AC平行与y轴,BC平行与x轴,得到AC与BC垂直,由A与B的坐标分别求出AC与BC的长,利用勾股定理求出AB的长,即可求出三角形的面积与周长.
解答:解:将两函数解析式联立得:
,
解得:
或
,
∴A(
,
),B(-
,-
),
∵AC∥y轴,BC∥x轴,
∴△ABC为直角三角形,
∴AC=2
,BC=
,
根据勾股定理得:AB=
=5
,
则S△ABC=
AC•BC=10;周长为AC+BC+AB=2
+
+5
=3
+5
.
|
解得:
|
|
∴A(
| ||
| 2 |
| 10 |
| ||
| 2 |
| 10 |
∵AC∥y轴,BC∥x轴,
∴△ABC为直角三角形,
∴AC=2
| 10 |
| 10 |
根据勾股定理得:AB=
| AC2+BC2 |
| 2 |
则S△ABC=
| 1 |
| 2 |
| 10 |
| 10 |
| 2 |
| 10 |
| 2 |
点评:此题考查了一次函数与反比例函数的交点问题,涉及的知识有:平行线的性质,勾股定理,坐标与图形性质,解题的关键是得出△ABC为直角三角形.

练习册系列答案
相关题目
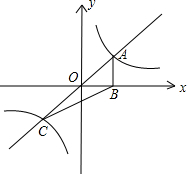 如图,正比例函数y=kx(k>0)与反比例函数y=
如图,正比例函数y=kx(k>0)与反比例函数y=| 1 |
| x |
| A、S=1 | B、S=2 |
| C、S=3 | D、S的值不能确定 |
 如图,正比例函数
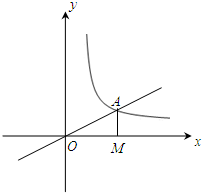
如图,正比例函数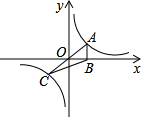 如图,正比例函数y=kx(k>0)与反比例函数y=
如图,正比例函数y=kx(k>0)与反比例函数y= 作x轴的垂线,垂足为M,已知△AOM的面积为1,点B(-1,t)为反比例函数在第三象限图象上的点.
作x轴的垂线,垂足为M,已知△AOM的面积为1,点B(-1,t)为反比例函数在第三象限图象上的点. 已知:如图,正比例函数y=k1x的图象与反比例函数
已知:如图,正比例函数y=k1x的图象与反比例函数