题目内容
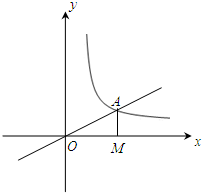 如图,正比例函数y=
如图,正比例函数y=| 1 |
| 2 |
| k |
| x |
(1)求反比例函数的解析式;
(2)如果B为反比例函数在第一象限图象上的点,且B点的横坐标为1,在x轴上求一点P,使PA+PB最小.(只需在图中作出点B,P,保留痕迹,不必写出理由)
分析:(1)A点在反比例函数上,三角形OAM的面积=
,三角形的面积已知,k可求出来,从而确定解析式.
(2)三点在同一直线上,PA+PB最小,找A关于x的对称点C,连接BC,与x轴的交点,即为所求的点.
| k |
| 2 |
(2)三点在同一直线上,PA+PB最小,找A关于x的对称点C,连接BC,与x轴的交点,即为所求的点.
解答: 解:(1)设A点的坐标为(a,b),则由
解:(1)设A点的坐标为(a,b),则由
ab=1,得ab=2=k,
∴反比例函数的解析式为y=
;
(2)由条件知:两函数的交点为
,
解得:
,
,
∴A点坐标为:(2,1),作出关于A点x轴对称点C点,连接BC,
P点即是所求见右图.
 解:(1)设A点的坐标为(a,b),则由
解:(1)设A点的坐标为(a,b),则由| 1 |
| 2 |
∴反比例函数的解析式为y=
| 2 |
| x |
(2)由条件知:两函数的交点为
|
解得:
|
|
∴A点坐标为:(2,1),作出关于A点x轴对称点C点,连接BC,
P点即是所求见右图.
点评:本题考查反比例函数的综合运用,关键知道反比例函数上的点和坐标轴构成的面积和k的关系,以及两个线段的和最短的问题.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
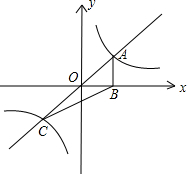 如图,正比例函数y=kx(k>0)与反比例函数y=
如图,正比例函数y=kx(k>0)与反比例函数y=| 1 |
| x |
| A、S=1 | B、S=2 |
| C、S=3 | D、S的值不能确定 |
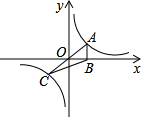 如图,正比例函数y=kx(k>0)与反比例函数y=
如图,正比例函数y=kx(k>0)与反比例函数y= 作x轴的垂线,垂足为M,已知△AOM的面积为1,点B(-1,t)为反比例函数在第三象限图象上的点.
作x轴的垂线,垂足为M,已知△AOM的面积为1,点B(-1,t)为反比例函数在第三象限图象上的点. 已知:如图,正比例函数y=k1x的图象与反比例函数
已知:如图,正比例函数y=k1x的图象与反比例函数