题目内容
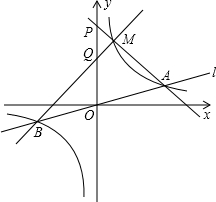
如图,直线y=x与反比例函数y=
(x>0)的图象交于点A,AB⊥y轴,垂足为B,点C在射线BA上(端点除外),点E在x轴上,且∠OCE=90°,CH⊥x轴,垂足为H,并与反比例函数y=
图象交于点G.
(1)若点B的坐标为(0,4),求k的值;
(2)在(1)的条件下,求证:HG=HE.

| k |
| x |
| k |
| x |
(1)若点B的坐标为(0,4),求k的值;
(2)在(1)的条件下,求证:HG=HE.

(1)∵点B的坐标为(0,4),AB⊥y轴,
∴点A的纵坐标为4,
∵点A在直线y=x上,
∴点A的坐标为(4,4),
把A(4,4)代入y=
得k=4×4=16;
(2)证明:反比例函数的解析式为y=
,
设H点坐标为(a,0),
∵CH⊥x轴,
∴C点坐标为(a,4),G点坐标为(a,
),
∴GH=
,
∵∠CHO=∠OCE=90°,
∴∠OHC-∠HOC=∠OCE-∠EOC,即∠OCH=∠CEH,
∴Rt△OCH∽Rt△CEH,
∴OH:CH=CH:EH,
∴EH=
,
∵OH=a,CH=4,
∴EH=
,
∴HG=HE.
∴点A的纵坐标为4,
∵点A在直线y=x上,
∴点A的坐标为(4,4),
把A(4,4)代入y=
| k |
| x |
(2)证明:反比例函数的解析式为y=
| 16 |
| x |
设H点坐标为(a,0),
∵CH⊥x轴,
∴C点坐标为(a,4),G点坐标为(a,
| 16 |
| a |
∴GH=
| 16 |
| a |
∵∠CHO=∠OCE=90°,
∴∠OHC-∠HOC=∠OCE-∠EOC,即∠OCH=∠CEH,
∴Rt△OCH∽Rt△CEH,
∴OH:CH=CH:EH,
∴EH=
| CH2 |
| OH |
∵OH=a,CH=4,
∴EH=
| 16 |
| a |
∴HG=HE.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目








 不变时,气球内气体的气压P(KPa)是气体体积V(m3)的反比例函数,其图象如图所示.
不变时,气球内气体的气压P(KPa)是气体体积V(m3)的反比例函数,其图象如图所示.