题目内容
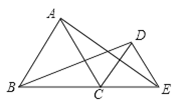
已知:四边形ABCD中,AD∥BC,AD=AB=CD,∠BAD=120°,点E是射线CD上的一个动点(与C、D不重合),将△ADE绕点A顺时针旋转120°后,得到△ABE',连接EE'.
(1)如图1,∠AEE'= °;
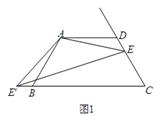
(2)如图2,如果将直线AE绕点A顺时针旋转30°后交直线BC于点F,过点E作EM∥AD交直线AF于点M,写出线段DE、BF、ME之间的数量关系;
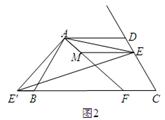
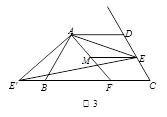
(3)如图3,在(2)的条件下,如果CE=2,AE=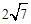 ,求ME的长.
,求ME的长.
(1)如图1,∠AEE'= °;

(2)如图2,如果将直线AE绕点A顺时针旋转30°后交直线BC于点F,过点E作EM∥AD交直线AF于点M,写出线段DE、BF、ME之间的数量关系;

(3)如图3,在(2)的条件下,如果CE=2,AE=
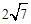 ,求ME的长.
,求ME的长. 
(1)∠AEE'=30°;
(2)当点E在线段CD上时, ;
;
当点E在CD的延长线上时,
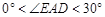 时,
时,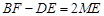 ;
;
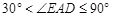 时,
时, ;
;
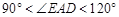 时,
时, ;
;
(3)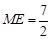 .
.
(2)当点E在线段CD上时,
 ;
; 当点E在CD的延长线上时,
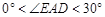 时,
时,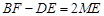 ;
;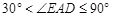 时,
时, ;
; 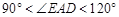 时,
时, ;
;(3)
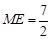 .
.试题分析:(1)根据旋转性质及三角形内角和定理即可;
(2)根据题意得到AN=
 E'N,EN=
E'N,EN= NE',再ME∥BC,得到
NE',再ME∥BC,得到 ,从而得到线段DE、BF、ME之间的数量关系;
,从而得到线段DE、BF、ME之间的数量关系;(3)通过作辅助线,求出
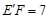 ,再由(2)的结论得到ME的长.
,再由(2)的结论得到ME的长.试题解析:(1)根据题意知:AE=AE' ,∠E'AE=120°,所以∠AEE'=30°;
(2)当点E在线段CD上时,设AF与EE'相交于N,
∵∠E'AE=120°,∠EAF=30°,
∴∠E'AN=90°,∠AE'N=30°,
∴AN=
 E'N,
E'N,∵∠NAE=∠NEA=30°,
∴AN=EN,即EN=
 NE',
NE',∵ME∥BC
∴△MNE∽△FNE'
∴
 ,而E'B=DE,
,而E'B=DE,∴
 ;
; 同理:当点E在CD的延长线上,
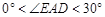 时,
时,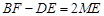 ;
;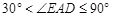 时,
时, ;
; 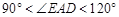 时,
时, ;
;(3)作
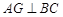 于点G, 作
于点G, 作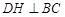 于点H.
于点H.
由AD∥BC,AD=AB=CD,∠BAD=120°,得∠ABC=∠DCB=60°,
易知四边形AGHD是矩形和两个全等的直角三角形
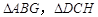 .
.则GH="AD" , BG=CH.
∵
 ,
,∴点
 、B、C在一条直线上.
、B、C在一条直线上.设AD=AB=CD=x,则GH=x,BG=CH=
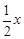 ,.
,.作
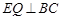 于Q.
于Q.在Rt△EQC中,CE="2,"
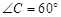 ,
,∴
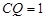 ,
, 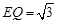 .
.∴E'Q=
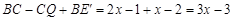 .
.作
 于点P.
于点P. ∵△ADE绕点A顺时针旋转120°后,得到△ABE'.
∴△AEE'是等腰三角形,
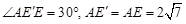 .
.∴在Rt△APE'中,E'P=
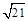 .
.∴EE'=2E'P=
 .
. ∴在Rt△EQ E'中,E'Q=
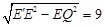 .
. ∴
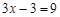 .
.∴
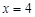 .
.∴
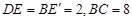 ,
,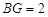 .
.∴
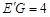
在Rt△E'AF中,
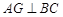 ,
,∴Rt△AG E'∽Rt△FA E'.
∴
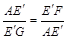
∴
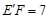 .
.∴
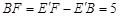 .
.由(2)知:

∴
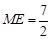 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+