题目内容
已知直角坐标系中菱形ABCD的位置如图,C、D两点的坐标分别为(8,0)、(0,6).现有两动点P、Q分别从A、C同时出发,点P沿折线ADC向终点C运动, 点Q沿线段CA向终点A运动,当P、Q两点中有一点到达终点时,另一点也立即停止运动,设运动时间为t秒.

(1)填空:菱形ABCD的边长是 ,面积是 ;
(2)探究下列问题:
①若点P的速度为每秒2.5个单位,点Q的速度为每秒3个单位,求△APQ的面积S关于t的函数关系式,并求出S的最大值;
②在运动过程中,能否使得△APQ绕它的一边中点旋转180°,旋转前后两个三角形组成的四边形为矩形,若存在,求出t的值;若不存在,请说明理由.

(1)填空:菱形ABCD的边长是 ,面积是 ;
(2)探究下列问题:
①若点P的速度为每秒2.5个单位,点Q的速度为每秒3个单位,求△APQ的面积S关于t的函数关系式,并求出S的最大值;
②在运动过程中,能否使得△APQ绕它的一边中点旋转180°,旋转前后两个三角形组成的四边形为矩形,若存在,求出t的值;若不存在,请说明理由.
(1)10,24;(2)①S最大=16;② 或
或 .
.
 或
或 .
.试题分析:(1)根据勾股定理可求得菱形ABCD的边长是10,用菱形的面积公式即可求出面积;
(2)①分情况讨论P点的位置,借助三角形相似进行计算;
②分别讨论当∠APQ=90°时,当∠AQP=90°时,t的取值即可.
试题解析:(1)10,24;
(2)①当P点在AD上时(0<t<4)
由题意,得AP=2.5t,AQ=16-3t.
如图1,过点P作PG⊥AC,垂足为G,则 △APG∽△ADO,

∴
 ,
,∴PG=
 ,
, ∴
 .
.当P点在CD上时,Q先到终点,故

AD+DP=2.5t,CQ==3t,则AQ=16-3t,CP=20-2.5t,
过点P作PG⊥AC,垂足为G,则 △PCH∽△DCO,

∴
 ,
,∴PH=12-
 ,
, ∴
 .
.当0<t<4时,
 ,
,当4≤t<
 时,对称轴为t=
时,对称轴为t= ,
,根据二次函数的增减性t=4,S最大=12,
综上可知:S最大="16" ;
②∵△APQ绕它的一边中点旋转180°,旋转前后两个三角形组成的四边形为矩形,
∴△APQ为直角三角形.
当∠APQ=90°时,

AP=2.5t,CQ=3t,则AQ=16-3t.
∵∠APQ=∠AOD=90°
∠PAQ=∠DAO
∴△APG∽△ADO,
∴
 ,
,∴

∴

当∠AQP=90°时,

AP=2.5t,CQ=3t,则AQ=16-3t.
∵∠AQP=∠AOD=90°
∠PAQ=∠DAO
∴△APG∽△ADO,
∴
 ,
,∴

∴

∴当
 或
或 时,△APQ绕它的一边中点旋转180°,旋转前后两个三角形组成的四边形为矩形.
时,△APQ绕它的一边中点旋转180°,旋转前后两个三角形组成的四边形为矩形.
练习册系列答案
相关题目
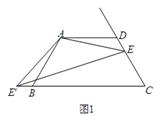
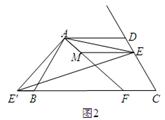
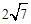 ,求ME的长.
,求ME的长. 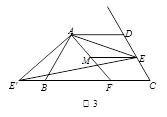

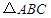 绕点
绕点 按逆时针方向旋转,旋转角为
按逆时针方向旋转,旋转角为 ,旋转后使各边长变为原来的
,旋转后使各边长变为原来的 倍,得到
倍,得到 ,我们将这种变换记为[
,我们将这种变换记为[ ].
]. ]得
]得 :
: = ___;直线
= ___;直线 与直线
与直线 所夹的锐角为 __ °;
所夹的锐角为 __ °;
 ,对
,对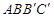 为梯形,其中
为梯形,其中 ∥
∥ ,求
,求 和
和



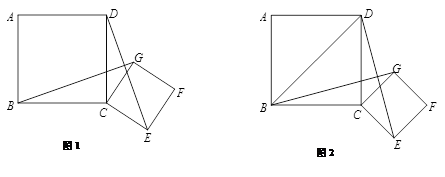
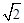 ,将正方形CEFG绕着点C旋转到某一位置时恰好使得CG//BD,BG=BD.
,将正方形CEFG绕着点C旋转到某一位置时恰好使得CG//BD,BG=BD.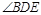 的度数;
的度数;