Question

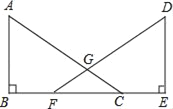
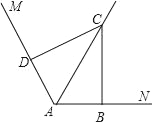
【题目】（1）如图，已知∠MAN＝120°，AC平分∠MAN，∠ABC＝∠ADC＝90°，则能得到如下两个结论：①DC＝BC；②AD+AB＝AC． 请你证明结论②．

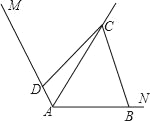
（2）如图，把（1）中的条件“∠ABC＝∠ADC＝90°”改为∠ABC+∠ADC＝180°，其他条件不变，则（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．

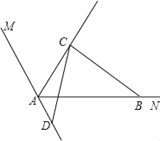
（3）如图3，如果D在AM的反向延长线上，把（1）中的条件“∠ABC＝∠ADC＝90°”改为∠ABC＝∠ADC，其他条件不变，（1）中的结论是否仍然成立？若成立，请直接回答；若不成立，你又能得出什么结论，直接写出你的结论．

Answer 1

【答案】（1）见解析；（2）（1）中的结论仍然成立，证明见解析；（3）①DC＝BC成立；②不成立，AB﹣AD＝AC．

【解析】

（1）由已知易证得△ADC≌△ABC，可得AD＝AB，根据已知可得∠ACD＝30°可得AC＝2AD，即可得结论．

（2）以上结论仍成立；作辅助线CE⊥AD，CF⊥AB，首先证得△ACF≌△ACE，可得CF＝CE，即可证得△CFB≌△CED，即可得（1）中结论．

（3）同（2）理作辅助线可得DC＝BC成立，AB﹣AD＝AC．

解：（1）∵AC平分∠MAN，

∴∠DAC＝∠BAC＝60°，

∵∠ABC＝∠ADC＝90°，AC为公共边，

∴△ADC≌△ABC（AAS），

∴AD＝AB，DC＝BC①；

∵∠DCA＝30°，

∴AC＝2AD＝AD+AB②；

（2）如图：作辅助线CF⊥AB，CE⊥AD，

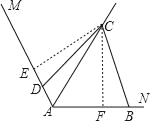
∵AC平分∠MAN，

∴∠DAC＝∠BAC＝60°，

又∵CF⊥AB，CE⊥AD，且AC为公共边，

∴△ACF≌△ACE（AAS），即CF＝CE①；

∵∠ABC+∠ADC＝180°，∠MAN＝120°，

∴∠DCB＝180°﹣120°＝60°，

∵在直角三角形AFC中∠ACF＝30°，

∴∠DCA+∠FCB＝30°，

∵在直角三角形AEC中∠DCA+∠DCE＝30°，

∴∠FCB＝∠DCE②；

由CE⊥AD，CF⊥AB，且已证得条件①②，

∴△CED≌△CFB（ASA），

∴DC＝BC；ED＝FB；

∵在直角△ACF中，AC＝2AF，在直角△ACE中，AC＝2AE，即AC＝AE+AF，

已证得ED＝FB，

∴AC＝AD+AB；

（3）①DC＝BC成立；②不成立，AB﹣AD＝AC．

故答案为：（1）见解析；（2）（1）中的结论仍然成立，证明见解析；（3）①DC＝BC成立；②不成立，AB﹣AD＝AC．