题目内容
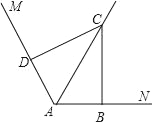
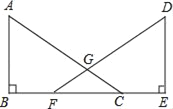
【题目】已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE.
求证:GF=GC.
【答案】证明见解析
【解析】
由AB⊥BE和DE⊥BE可得∠B=∠E=90°,由此可得△ABC和△DEF是直角三角形;又由BF=CE可得CB=EF,再加条件AC=DF,可以用HL定理证明Rt△ABC≌Rt△DEF,由此可以得到∠ACB=∠DFE,利用等角对等边可证出GF=GC.
证明:∵AB⊥BE
∴∠B=90°
∵DE⊥BE
∴∠E=90°
∵BF=CE
∴BF+CF=CE+CF
即:CB=EF
在Rt△ABC和Rt△DEF中![]() ,
,
∴Rt△ABC≌Rt△DEF(HL)
∴∠ACB=∠DFE
∴GF=CG.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
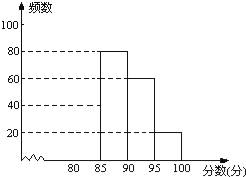
【题目】某校组织了“安全在我心中”知识竞赛活动.根据获奖同学在竞赛中的成绩制成的统计图表如下:
分数段 | 频数 | 频率 |
80≤x<85 | x | 0.2 |
85≤x<90 | 80 | y |
90≤x<95 | 60 | 0.3 |
95≤x<100 | 20 | 0.1 |
根据以上图表提供的信息,解答下列问题:
(1)写出表中x,y的数值;
(2)请补全频数分布直方图;
(3)如果成绩在95分以上(含95分)的可以获得特等奖,那么获奖的同学获得特等奖的概率是多少?
(4)获奖成绩的中位数落在哪个分数段?