题目内容
【题目】已知抛物线![]() (
(![]() 为常数,
为常数,![]() )经过点
)经过点![]() ,点
,点![]() 是
是![]() 轴正半轴上的动点.
轴正半轴上的动点.
(Ⅰ)当![]() 时,求抛物线的顶点坐标;
时,求抛物线的顶点坐标;
(Ⅱ)点![]() 在抛物线上,当
在抛物线上,当![]() ,
,![]() 时,求
时,求![]() 的值;
的值;
(Ⅲ)点![]() 在抛物线上,当
在抛物线上,当![]() 的最小值为
的最小值为![]() 时,求
时,求![]() 的值.
的值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
(Ⅰ)把b=2和点![]() 代入抛物线的解析式,求出c的值,进行配方即可得出顶点坐标
代入抛物线的解析式,求出c的值,进行配方即可得出顶点坐标
(Ⅱ)根据点![]() 和)点
和)点![]() 在抛物线上和
在抛物线上和![]() 得出点
得出点![]() 在第四象限,且在抛物线对称轴
在第四象限,且在抛物线对称轴![]() 的右侧.过点
的右侧.过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,则点
,则点![]() ,再根据D、E两点坐标得出
,再根据D、E两点坐标得出![]() 为等腰直角三角形,得出
为等腰直角三角形,得出![]() ,再根据已知条件
,再根据已知条件![]() ,
,![]() ,从而求出b的值
,从而求出b的值
(Ⅲ)根据点![]() 在抛物线上得出点
在抛物线上得出点![]() 在第四象限,且在直线
在第四象限,且在直线![]() 的右侧;取点
的右侧;取点![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,![]() 与
与![]() 轴相交于点
轴相交于点![]() ,得出
,得出![]() ,此时
,此时![]() 的值最小;过点
的值最小;过点![]() 作
作![]() 轴于点
轴于点![]() ,则点
,则点![]() .再根据
.再根据![]() 得出m与b的关系,然后根据两点间的距离公式和
得出m与b的关系,然后根据两点间的距离公式和
![]() 的最小值为
的最小值为![]() ,列出关于b的方成即可
,列出关于b的方成即可
解:(Ⅰ)∵抛物线![]() 经过点
经过点![]() ,
,
∴![]() .即
.即![]() .
.
当![]() 时,
时,![]() ,
,
∴抛物线的顶点坐标为![]() .
.
(Ⅱ)由(Ⅰ)知,抛物线的解析式为![]() .
.
∵点![]() 在抛物线
在抛物线![]() 上,
上,
∴![]() .
.
由![]() ,得
,得![]() ,
,![]() ,
,
∴点![]() 在第四象限,且在抛物线对称轴
在第四象限,且在抛物线对称轴![]() 的右侧.
的右侧.
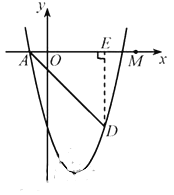
如图,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,则点
,则点![]() .
.
∴![]() ,
,![]() .得
.得![]() .
.
∴在![]() 中,
中,![]() .
.
∴![]() .
.
由已知![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
(Ⅲ)∵点![]() 在抛物线
在抛物线![]() 上,
上,
∴![]() .
.
可知点![]() 在第四象限,且在直线
在第四象限,且在直线![]() 的右侧.
的右侧.
考虑到![]() ,可取点
,可取点![]() ,
,
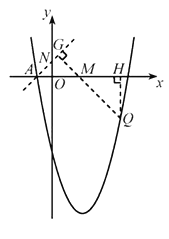
如图,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,![]() 与
与![]() 轴相交于点
轴相交于点![]() ,
,
有![]() ,得
,得![]() ,
,
则此时点![]() 满足题意.
满足题意.
过点![]() 作
作![]() 轴于点
轴于点![]() ,则点
,则点![]() .
.
在![]() 中,可知
中,可知![]() .
.
∴![]() ,
,![]() .
.
∵点![]() ,
,
∴![]() .解得
.解得![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.

练习册系列答案
相关题目