题目内容
【题目】求证:等腰三角形两腰上的中线相等.
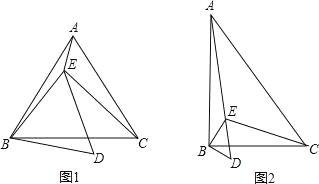
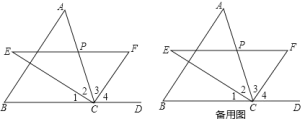
(1)请用尺规作出△ABC两腰上的中线BD、CE(保留痕迹,不写作法);
(2)结合图形,写出已知、求证和证明过程.
【答案】(1)作图见解析;(2)见解析.
【解析】
(1)分别作AB、AC的垂直平分线得到AB、AC的中点E、D,从而得到AB、AC边上的中线CE 、BD;
(2)结合图形写出已知,求证,然后再根据已知和图形进行证明.可根据等腰三角形的性质得出相关的等角或相等的线段:DC=BE,∠DCB=∠EBC,BC=CB,可证明△BDC≌△CEB,所以BD=CE,即等腰三角形的两腰上的中线相等.
(1)如图,CE 、BD分别为AB、AC边上的中线;
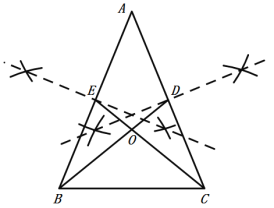
(2)已知:△ABC中,AB=AC,AD=DC,AE=EB,
求证:BD=CE.
证明:∵AB=AC,AD=DC,AE=EB,
∴AD = AE,
在△ABD与△ACE中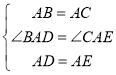 ,
,
∴△ABD![]() △ACE(SAS).
△ACE(SAS).
∴BD=CE.
即等腰三角形的两腰上的中线相等.

练习册系列答案
相关题目