题目内容
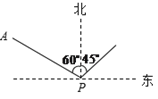
【题目】如图,小岛在港口P的北偏西60°方向,距港口56海里的A处,货船从港口P出发,沿北偏东45°方向匀速驶离港口P,4小时后货船在小岛的正东方向。求货船的航行速度。(精确到0.1海里/时,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
【答案】货船的航行速度约为9.9海里/时
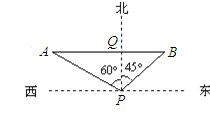
【解析】试题分析:由已知可得AB⊥PQ,∠QAP=60°,∠A=30°,AP=56海里,要求货船的航行速度,即是求PB的长,可先在直角三角形APQ中利用三角函数求出PQ,然后利用三角函数求出PB即可.
试题解析:解:设货船速度为x海里/时,4小时后货船在点B处,作PQ⊥AB于点Q.
由题意AP=56海里,PB=4x海里,在直角三角形APQ中,∠APQ=60°,所以PQ=28.
在直角三角形PQB中,∠BPQ=45°,所以,PQ=PB×cos45°=2![]() x.
x.
所以,2![]() x=28,解得:x=7
x=28,解得:x=7![]() ≈9.9.
≈9.9.
答:货船的航行速度约为9.9海里/时.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目